Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.
Câu hỏi
🗣️ Nguyễn Trí Minh hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
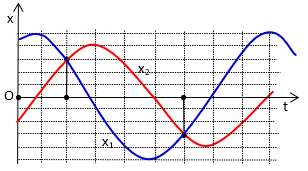
Hai vật A và B dao động điều hòa cùng tần số. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ x1 của A và li độ x2 của B theo thời gian t. Hai dao động của A và B lệch pha nhau:
(A) 0,20 rad.
(B) 1,49 rad
(C) 1,70 rad.
(D) 1,65 rad.
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: ,2023, de thi thu vat li thpt tran phu co dap an.
Câu trả lời hay nhất
🕵 Bạn Vũ Văn Hiển trả lời:
Chọn câu (D): 1,65 rad.
Xét dao động \({x_1}\) : Pha dao động tại thời điểm \({t_1}\) : \({\mathop{\rm Cos}\nolimits} (\omega .{t_1} + {\varphi _1}) = \frac{{{x_1} = 3\,o\^a }}{{A = 5\,o\^a }} \Rightarrow \omega .{t_1} + {\varphi _1} = \pm {\cos ^{ - 1}}(\frac{3}{5}) + k2\pi \) Tại thời điểm \({t_1}\) : Vật 1 đang chuyển động về vị trí cân bằng theo chiều âm, nên pha dao động phải dương. Do đó, \(\omega .{t_1} + {\varphi _1} = {\cos ^{ - 1}}(\frac{3}{5}) + k2\pi \) Xét dao động \({x_2}\) : Pha dao động tại thời điểm \({t_1}\) : \({\mathop{\rm Cos}\nolimits} (\omega .{t_1} + {\varphi _2}) = \frac{{{x_1} = 3\,o\^a }}{{A = 4\,o\^a }} \Rightarrow \omega .{t_1} + {\varphi _2} = \pm {\cos ^{ - 1}}(\frac{3}{4}) + k2\pi \) Tại thời điểm \({t_1}\) : Vật 2 đang chuyển động đến vị trí biên dương nên pha dao động phải âm. Do đó, \(\omega .{t_1} + {\varphi _2} = - {\cos ^{ - 1}}(\frac{3}{4}) + k2\pi \) Độ lệch pha giữa hai dao động là: \(\Delta \varphi = {\varphi _2} - {\varphi _1} = - {\cos ^{ - 1}}(\frac{3}{4}) - {\cos ^{ - 1}}(\frac{3}{5}) = - \,1,65(rad)\) . Giải 2: Từ đồ thị, ta có biên độ: A1=5 ô ; A2 = 4 ô Xét lúc 2 dao động cùng có li độ: x1 =x2 =3 ô. Dùng vòng tròn lượng giác: Độ lệch pha của 2 dao động: \[\begin{array}{l}\Delta \varphi = {\alpha _1} + {\alpha _2} = {\cos ^{ - 1}}(\frac{3}{5}) + {\cos ^{ - 1}}(\frac{3}{4})\\ = 0.927 + 0,7227 = 1,649\;rad\end{array}\]
![Xét dao động \({x_1}\) : Pha dao động tại thời điểm \({t_1}\) :
\({\mathop{\rm Cos}\nolimits} (\omega .{t_1} + {\varphi _1}) = \frac{{{x_1} = 3\,o\^a }}{{A = 5\,o\^a }} \Rightarrow \omega .{t_1} + {\varphi _1} = \pm {\cos ^{ - 1}}(\frac{3}{5}) + k2\pi \)
Tại thời điểm \({t_1}\) : Vật 1 đang chuyển động về vị trí cân bằng theo chiều âm, nên pha dao động phải dương. Do đó, \(\omega .{t_1} + {\varphi _1} = {\cos ^{ - 1}}(\frac{3}{5}) + k2\pi \)
Xét dao động \({x_2}\) : Pha dao động tại thời điểm \({t_1}\) :
\({\mathop{\rm Cos}\nolimits} (\omega .{t_1} + {\varphi _2}) = \frac{{{x_1} = 3\,o\^a }}{{A = 4\,o\^a }} \Rightarrow \omega .{t_1} + {\varphi _2} = \pm {\cos ^{ - 1}}(\frac{3}{4}) + k2\pi \)
Tại thời điểm \({t_1}\) : Vật 2 đang chuyển động đến vị trí biên dương nên pha dao động phải âm. Do đó, \(\omega .{t_1} + {\varphi _2} = - {\cos ^{ - 1}}(\frac{3}{4}) + k2\pi \)
Độ lệch pha giữa hai dao động là:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = - {\cos ^{ - 1}}(\frac{3}{4}) - {\cos ^{ - 1}}(\frac{3}{5}) = - \,1,65(rad)\)
.
Giải 2:
Từ đồ thị, ta có biên độ:
A1=5 ô ; A2 = 4 ô
Xét lúc 2 dao động cùng có li độ:
x1 =x2 =3 ô.
Dùng vòng tròn lượng giác:
Độ lệch pha của 2 dao động:
\[\begin{array}{l}\Delta \varphi = {\alpha _1} + {\alpha _2} = {\cos ^{ - 1}}(\frac{3}{5}) + {\cos ^{ - 1}}(\frac{3}{4})\\ = 0.927 + 0,7227 = 1,649\;rad\end{array}\]](/images/cau-hoi-5/tra-loi-hai-vat-a-va-b-dao-dong-dieu-hoa-cung-tan-so-hinh-0-23091.png)
![Xét dao động \({x_1}\) : Pha dao động tại thời điểm \({t_1}\) :
\({\mathop{\rm Cos}\nolimits} (\omega .{t_1} + {\varphi _1}) = \frac{{{x_1} = 3\,o\^a }}{{A = 5\,o\^a }} \Rightarrow \omega .{t_1} + {\varphi _1} = \pm {\cos ^{ - 1}}(\frac{3}{5}) + k2\pi \)
Tại thời điểm \({t_1}\) : Vật 1 đang chuyển động về vị trí cân bằng theo chiều âm, nên pha dao động phải dương. Do đó, \(\omega .{t_1} + {\varphi _1} = {\cos ^{ - 1}}(\frac{3}{5}) + k2\pi \)
Xét dao động \({x_2}\) : Pha dao động tại thời điểm \({t_1}\) :
\({\mathop{\rm Cos}\nolimits} (\omega .{t_1} + {\varphi _2}) = \frac{{{x_1} = 3\,o\^a }}{{A = 4\,o\^a }} \Rightarrow \omega .{t_1} + {\varphi _2} = \pm {\cos ^{ - 1}}(\frac{3}{4}) + k2\pi \)
Tại thời điểm \({t_1}\) : Vật 2 đang chuyển động đến vị trí biên dương nên pha dao động phải âm. Do đó, \(\omega .{t_1} + {\varphi _2} = - {\cos ^{ - 1}}(\frac{3}{4}) + k2\pi \)
Độ lệch pha giữa hai dao động là:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = - {\cos ^{ - 1}}(\frac{3}{4}) - {\cos ^{ - 1}}(\frac{3}{5}) = - \,1,65(rad)\)
.
Giải 2:
Từ đồ thị, ta có biên độ:
A1=5 ô ; A2 = 4 ô
Xét lúc 2 dao động cùng có li độ:
x1 =x2 =3 ô.
Dùng vòng tròn lượng giác:
Độ lệch pha của 2 dao động:
\[\begin{array}{l}\Delta \varphi = {\alpha _1} + {\alpha _2} = {\cos ^{ - 1}}(\frac{3}{5}) + {\cos ^{ - 1}}(\frac{3}{4})\\ = 0.927 + 0,7227 = 1,649\;rad\end{array}\]](/images/cau-hoi-5/tra-loi-hai-vat-a-va-b-dao-dong-dieu-hoa-cung-tan-so-hinh-1-17459.png)
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Bùi Văn Anh viết:
Chọn C, 1,70 rad.
👤 Đặng Văn Minh viết:
Chọn D, 1,65 rad.
➥ 🗣️ Nguyễn Trí Minh trả lời: Cảm ơn bạn, câu này hình như có trong file doc này (2023) Đề thi thử Vật Lí THPT Trần Phú có đáp án
👤 Trương Văn Phúc viết:
Chọn B, 1,49 rad
👤 Phan Văn Minh viết:
Chọn A, 0,20 rad.
👤 Nguyễn Hải Lộc viết:
Chọn D: 1,65 rad.
Gửi bạn các file hữu ích đi kèm câu hỏi:
- (2023) Đề thi thử Vật Lí THPT Trần Phú có đáp án (.doc)
- (2023) Đề thi thử Vật Lí THPT Trần Phú - Vĩnh Phúc (Lần 1) có đáp án (.doc)
- (2023) Đề thi thử Vật lí THPT soạn theo ma trận đề minh họa BGD (Đề 15) có đáp án (.doc)
- (2023) Đề thi thử Vật lí THPT soạn theo ma trận đề minh họa BGD (Đề 17) có đáp án (.doc)
- (2023) Đề thi thử Vật Lí THPT Phú Dực - Thái Bình (Lần 1) có đáp án (.doc)
- (2023) Đề thi thử Vật lí THPT soạn theo ma trận đề minh họa BGD (Đề 16) có đáp án (.doc)
- Sơ đồ sự phân bố thời gian chuyển động của vật trên quỹ đạo khi dao động
- Galileo và bản chất của khoa học vật lí
