Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.
Câu hỏi
🗣️ Trần Văn Phú hỏi: Cho mình hỏi một câu Trắc nghiệm Vật Lý lớp 12 trong sách bài tập
Hình bên là đồ thị biểu diễn sự phụ thuộc của vận tốc v theo thời gian t của một vật dao động điều hòa. Phương trình dao động của vật là
(A) \(x = \frac{3}{{8\pi }}\cos \left( {\frac{{40\pi }}{3}t + \frac{\pi }{6}} \right)\left( {cm} \right)\) .
(B) \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t + \frac{\pi }{6}} \right)\left( {cm} \right)\) .
(C) \(x = \frac{3}{{8\pi }}\cos \left( {\frac{{40\pi }}{3}t - \frac{\pi }{6}} \right)\left( {cm} \right)\) .
(D) \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)\left( {cm} \right)\) .
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: trac nghiem tong hop vat li 2023 co dap an.
Câu trả lời hay nhất
🕵 Bạn Nguyễn Thị Đức trả lời:
Chọn câu (D): \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)\left( {cm} \right)\) .
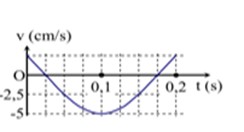
Lời giải Từ đồ thị ta có độ chia nhỏ nhất của mỗi ô là: 0,025 s Mặt khác: \[\frac{1}{2}\] chu kì ứng với 6 ô \( \Rightarrow \frac{T}{2} = 0,15\left( s \right) \Rightarrow T = 0,3\left( s \right) \Rightarrow \omega = \frac{{20\pi }}{3}\left( {rad/s} \right)\) Khi t = 0 thì \(v = \frac{{{v_{max}}}}{2}\) và đang giảm \( \Rightarrow \varphi = - \frac{\pi }{6}\) \(A = \frac{{{v_{max}}}}{\omega } = \frac{3}{{4\pi }}\left( {cm} \right)\) ⇒ \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)\left( {cm} \right)\) Đáp án đúng: D
![Lời giải
Từ đồ thị ta có độ chia nhỏ nhất của mỗi ô là: 0,025 s
Mặt khác: \[\frac{1}{2}\] chu kì ứng với 6 ô \( \Rightarrow \frac{T}{2} = 0,15\left( s \right) \Rightarrow T = 0,3\left( s \right) \Rightarrow \omega = \frac{{20\pi }}{3}\left( {rad/s} \right)\)
Khi t = 0 thì \(v = \frac{{{v_{max}}}}{2}\) và đang giảm \( \Rightarrow \varphi = - \frac{\pi }{6}\)
\(A = \frac{{{v_{max}}}}{\omega } = \frac{3}{{4\pi }}\left( {cm} \right)\) ⇒ \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)\left( {cm} \right)\) Đáp án đúng: D](/images/cau-hoi/tra-loi-hinh-ben-la-do-thi-bieu-dien-su-phu-thuoc-cua-van-toc-0-6991.jpg)
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Lê Thị Ngọc viết:
Chọn C, \(x = \frac{3}{{8\pi }}\cos \left( {\frac{{40\pi }}{3}t - \frac{\pi }{6}} \right)\left( {cm} \right)\) .
👤 Phạm Thị Vĩ viết:
Chọn D, \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)\left( {cm} \right)\) .
➥ 🗣️ Trần Văn Phú trả lời: Cảm ơn bạn, câu này hình như có trong file doc này Trắc nghiệm tổng hợp Vật lí 2023 có đáp án
👤 Trần Thị Linh viết:
Chọn B, \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t + \frac{\pi }{6}} \right)\left( {cm} \right)\) .
👤 Phạm Thị Hiển viết:
Chọn A, \(x = \frac{3}{{8\pi }}\cos \left( {\frac{{40\pi }}{3}t + \frac{\pi }{6}} \right)\left( {cm} \right)\) .
👤 Trần Văn Đức viết:
Chọn D: \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)\left( {cm} \right)\) .
Gửi bạn các file hữu ích đi kèm câu hỏi:
- Trắc nghiệm tổng hợp Vật lí 2023 có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 13. Tổng hợp lực – Phân tích lực có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 5. Tổng hợp và phân tích lực có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 13. Tổng hợp và phân tích lực. Cân bằng lực có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 5: Chuyển động tổng hợp (Phần 2) có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 2: Đồ thị độ dịch chuyển theo thời gian. Độ dịch chuyển tổng hợp và vận tốc tổng hợp có đáp án (.doc)
- Sơ đồ sự phân bố thời gian chuyển động của vật trên quỹ đạo khi dao động
- Các nhà vật lí vẫn bất đồng sâu sắc về ý nghĩa của cơ học lượng tử
