Giữa hai bến sông A, B có hai tàu chuyển thư chạy thẳng đều. Tàu đi từ A chạy xuôi dòng, tàu đi từ B chạy ngược dòng. Khi gặp nhau và chuyển thư, mỗi tàu

Câu hỏi

🗣️ Phạm Thị Thành hỏi: Cho mình hỏi một câu Trắc nghiệm Vật Lý lớp 12 trong sách bài tập

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: trac nghiem tong hop vat li 2023 co dap an.

Câu trả lời hay nhất

🕵 Bạn Lê Thị Nguyên trả lời:

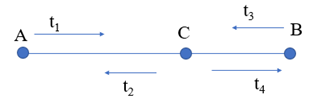
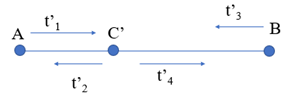
Lời giải Gọi C là điểm gặp nhau, v là vận tốc dòng nước. Theo đề bài: vận tốc 2 tàu so với dòng nước bằng nhau, ta gọi là V Vì hai tàu xuất phát cùng lúc và gặp nhau tại C nên t1 = t3 (1) Sau đó, 2 tàu quay trở lại tổng thời gian tàu A đi là 3 h, tàu B đi là 1,5 h. t1 + t2 = 3 h t3 + t4 = 1,5 h Thời gian đi của tàu từ A tới C: \({t_1} = \frac{{AC}}{{V + v}}\) Thời gian về của tàu từ C tới A: \({t_2} = \frac{{AC}}{{V - v}}\) Thời gian tàu đi từ A cả đi lẫn về là \({t_1} + {t_2} = 3 \Leftrightarrow \frac{{AC}}{{V + v}} + \frac{{AC}}{{V - v}} = AC\left( {\frac{1}{{V + v}} + \frac{1}{{V - v}}} \right)\, = 3\) (2)   Thời gian đi của tàu từ B tới C: \({t_3} = \frac{{BC}}{{V - v}}\) Thời gian về của tàu từ C tới B: \({t_4} = \frac{{BC}}{{V + v}}\) Thời gian tàu đi từ B cả đi lẫn về là \({t_3} + {t_4} = 1,5 \Leftrightarrow \frac{{BC}}{{V - v}} + \frac{{BC}}{{V + v}} = BC\left( {\frac{1}{{V - v}} + \frac{1}{{V + v}}} \right) = 1,5\) (3) Từ (2), (3) \( \Rightarrow AC = 2BC\) \( \Rightarrow AC = \frac{2}{3}AB\) thay vào (1) được: Mà thời gian đi của tàu từ A tới C bằng thời gian đi của tàu từ B tới C nên \(\frac{{AC}}{{V + v}}\)\( = \frac{{BC}}{{V - v}}\) \( \Rightarrow V = 3v\) Thay \(AC = \frac{2}{3}AB\) và V = 3v vào (2) \(\frac{2}{3}AB\left( {\frac{1}{{4v}} + \frac{1}{{2v}}} \right)\, = 3 \Rightarrow AB = 6v\) (4) Để thời gian cả đi lẫn về của hai tàu như nhau thì hai tàu gặp nhau ở vị trí C’ t’1 + t’2 = t’3 + t’4 \( \Rightarrow \frac{{AC'}}{{V + v}} + \frac{{AC'}}{{V - v}} = \frac{{BC'}}{{V - v}} + \frac{{BC'}}{{V + v}} \Rightarrow AC' = BC' = \frac{{AB}}{2}\) Khi xuất phát tàu B xuất phát trước tàu A một khoảng t0, ta có: \(t_3^' - t_1^' = {t_0}\)\( \Rightarrow \frac{{BC'}}{{V - v}} - \frac{{AC'}}{{V + v}} = {t_0}\) \( \Rightarrow BC'\left( {\frac{1}{{V - v}} - \frac{1}{{V + v}}} \right) = {t_0} \Rightarrow \frac{{AB}}{2}\left( {\frac{1}{{2v}} - \frac{1}{{4v}}} \right) = {t_0}\) Thay (4) vào \( \Rightarrow {t_0} = \frac{{6v}}{2}.\frac{1}{{4v}} = 0,75\,h\) Vậy tàu A phải xuất phát muộn hơn tàu B là 0,75 h = 45 phút

---

Câu trước | Câu kế tiếp

Gửi bạn các file hữu ích đi kèm câu hỏi:

• Tổng hợp các câu hỏi trắc nghiệm lý thuyết vật lí (.rar)
• Tổng hợp các câu trắc nghiệm đồ thị vật lí
• Tổng hợp các câu trắc nghiệm vật lí dạng đồ thị (.pdf)
• Trăc nghiệm tổng hợp vật lí 12 (.doc)
• TỔNG HỢP TOÀN BỘ LÍ THUYẾT + BÀI TẬP + TRẮC NGHIỆM LỚP 11 (.doc)
• 70 câu trắc nghiệm chương 2, 3 Lí 12 NC (có đáp án) (.doc)
• Tàng hình con tàu từ dòng nước chảy
• Trung Quốc phóng tàu thám hiểm mặt trăng thứ hai