- Andreas Müller (Tạp chí The Physics Teacher, tháng 1/2013)
Ở độ cao ban đầu nào thì vật rơi nhanh hơn tốc độ âm thanh?
Vào ngày 14 tháng 10, 2012, Felix Baumgartner, một nhà nhảy dù người Áo, đã lập kỉ lục thế giới mới về rơi tự do. Nhảy ra từ độ cao khoảng 39 km, ông đã đạt tới tốc độ tối đa 1342 km/h, trở thành người đầu tiên phá vỡ rào cản tốc độ âm thanh trong rơi tự do. Để hiểu được một vài phương diện vật lí thiết yếu của kì công này, chúng tôi tự hỏi tại sao ông phải bắt đầu nhảy từ độ cao đó (khi mà công sức bỏ ra để nhảy từ một độ cao như thế là rất nhiều, theo thông tin trên báo chí thì chi phí lên tới 50 triệu USD). Chính xác hơn, liệu bạn có thể đưa ra một ước tính cho độ cao ban đầu tối thiểu – cái chúng ta sẽ gọi là giới hạn Baumgartner, zB – của người nhảy dù muốn phá vỡ rào cản tốc độ âm thanh trong rơi tự do hay không ?
Xét gần đúng: Vận tốc tới hạn rơi tự do và khối lượng riêng của khí quyển
Tại cơ sở của bài toán của chúng ta là hai yếu tố vật lí chính, vận tốc tới hạn rơi tự do trong một môi trường cản, nó phụ thuộc vào khối lượng riêng của môi trường, và khối lượng riêng của khí quyển hóa ra lại phụ thuộc vào độ cao. Kết hợp hai sự phụ thuộc này sẽ cho phép chúng ta xác định độ cao giới hạn zB mà chúng ta đang quan tâm. Trước tiên, ta hãy nhắc lại kết quả cho vận tốc tới hạn của một vật chuyển động trong một môi trường cản1 (đồng thời mời tham khảo tư liệu 2 và 3 cho một trường hợp mở rộng, cũng đăng trên tạp chí này):
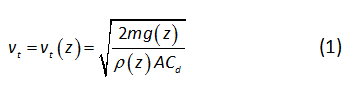
với m, A, Cd lần lượt là khối lượng, tiết diện, và hệ số cản của vật rơi, ρ là khối lượng riêng của môi trường mà vật rơi, và g là gia tốc trọng trường. Vận tốc tới hạn vt = vt(z) phụ thuộc vào độ cao z thông qua ρ = ρ(z) và g = g(z), nhưng ta có thể bỏ qua một cách an toàn sự phụ thuộc độ cao của g để xét gần đúng như dự tính ở đây4. Tỉ số của vận tốc tới hạn tại độ cao z và tại độ cao zero (mặt đất) khi đó là

(tại đây về sau, tất cả các đại lượng có chỉ số dưới 0 là chỉ tại mặt đất, z = 0.)
Tiếp theo, ta phải đưa ρ(z) vào; để lấy gần đúng như chúng ta đang quan tâm, ta có thể sử dụng “công thức phong vũ biểu” đã biết (hay mô hình “khí quyển theo hàm mũ”) cho mô hình của một khí quyển đẳng nhiệt5

với độ cao hS = kBT/Mg (kB = hằng số Boltzmann; T, M = nhiệt độ trung bình và khối lượng mol của khí quyển).
Kết hợp phương trình (2) và (3) và giải cho z, ta được

cho độ cao tại đó một vận tốc tới hạn cho trước có thể đạt tới. Áp dụng điều kiện vận tốc tới hạn này là bằng tốc độ âm thanh, tức là vt(z) = vS, ta thu được

Đây là độ cao mà trên đó vận tốc tới hạn có thể lớn hơn tốc độ âm thanh, nhưng nó chưa phải là giới hạn Baumgartner zB (đó là lí do vì sao nó mang dấu phẩy), vì chúng ta còn phải cộng thêm quãng đường rơi tự do mà trên quãng đường đó thật sự thu được vS:

(tất nhiên, từ s = ½ gt2, và t = v/g; xem phần thảo luận bên dưới về sự gần đúng vốn có trong phương pháp này). Các phương trình (5) và (6) kết hợp lại cho ta kết quả cuối cùng:
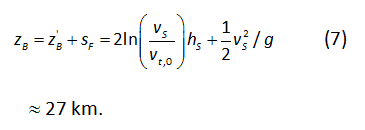
với z’B ≈ 22 km và sF ≈ 5 km là kết quả trung gian, và tốc độ âm thanh vS = 330 m/s, độ cao hS = 8,4 km (tại T = 288 K là nhiệt độ bề mặt trung bình của Trái Đất), và vận tốc tới hạn tại mặt đất vt,0 = 90 m/s làm dữ kiện tính toán. Những giá trị khác của những đại lượng này cũng thường được dùng tới, nhưng không mang lại sự thay đổi căn bản nào đối với sự gần đúng mà chúng ta đang xét.
Bàn luận
Sai số lớn nhất trong dữ kiện tính toán có lẽ nằm ở chỗ vt,0. Tính toán của chúng tôi sử dụng một giá trị được cung cấp bởi Wikipedia6 mới đây, nhưng những tài nguyên tham khảo khác7 thì nêu giá trị có phần thấp hơn. Một giá trị thấp hơn của vt,0 sẽ dẫn tới một giá trị lớn hơn của độ cao cần thiết để đạt tới vS (tức là giới hạn Baumgartner, zB).8 Với những gần đúng ở cấp độ của mô hình trên, một gần đúng bậc nhất là sử dụng sự phụ thuộc khối lượng riêng ρ(z) cho khí quyển đẳng nhiệt thay vì những mô hình thực tế hơn (hiệu chỉnh z’B). Nhưng gần đúng thô nhất là nằm ở chỗ sử dụng mô hình rơi tự do cho sF. Trong khi sức cản không khí là thấp ở gần độ cao ban đầu, nhưng nó không bằng không (kiểm tra cho sF với thời gian rơi thực tế trước khi đạt tới tốc độ âm thanh có thể tham khảo trên các bài báo). Lưu ý rằng hai hiệu chỉnh chính cho dữ kiện tính toán và cấp mô hình đều dẫn tới sự tăng zB đã cho ở đây, tức là tăng độ cao nhảy thật sự.
Xét những gần đúng và sai số có liên quan trong kết quả trên, ta thu được một giá trị
zB ≈ 30 km (8)
cho giới hạn Baumgartner, một giá trị lệch với độ cao nhảy trên thực tế khoảng 25%, nó hợp lí cho một phép tính gần đúng, và sự hiệu chỉnh là đúng hướng.
Tài liệu tham khảo
1. D. Halliday, và R. Resnick, J. Walker, Fundamentals of Physics (Wiley, New York, 2007), Chương 6.4.
2. I. Lovatt và B. Innes, “Resistance is not futile: Air resistance in an algebra-based course,” Phys. Teach. 43, 544 (11/ 2005).
3. N. Shea, “Terminal speed and atmospheric density,” Phys. Teach. 31, 176 (3/1993).
4. Lí do ở đây độc giả có thể tự suy luận.
5. Tài liệu 1, Chương 25.1.
6. en.wikipedia.org/wiki/Terminal_velocity.
7. G. Elert, “The Physics Factbook,” hypertextbook.com/facts/JianHuang.shtml.
8. Tốc độ âm thanh được hiểu ở đây là số đo tuyệt đối của vận tốc, với một giá trị tham chiếu cố định (ở điều kiện thường); tất nhiên, giá trị cục bộ tùy thuộc vào p và T, nhưng ở đây ta không xét trường hợp đó.
Trần Nghiêm dịch ◊