Chúng tôi trích giới thiệu với các bạn một số bản dịch từ tác phẩm Những câu hỏi và bài tập vật lí phổ thông của hai tác giả người Nga L. Tarasov và A. Tarasova, sách xuất bản ở Nga năm 1968. Bản dịch lại từ bản tiếng Anh xuất bản năm 1973.
Các bài giảng được trình bày dưới dạng thảo luận hỏi đáp giữa giáo viên và học sinh.
§14. Sự cân bằng của các vật
GV: Hai vị trí cân bằng của một viên gạch được thể hiện trên Hình 59. Cả hai vị trí cân bằng đó đều bền, nhưng mức độ bền của chúng khác nhau. Hỏi vị trí nào bền hơn?
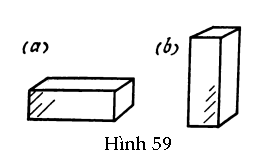
HS A: Rõ ràng là vị trí của viên gạch ở Hình 59a.
GV: Tại sao?
HS A: Trường hợp này trọng tâm của viên gạch ở gần mặt đất hơn.
GV: Chưa đủ đâu.
HS B: Vì diện tích mặt đế lớn hơn so với ở Hình 59b.
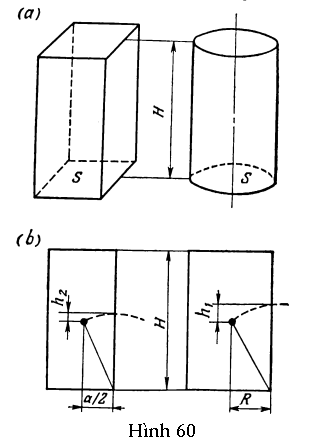
GV: Và như vậy vẫn chưa đủ. Để làm sáng tỏ vấn đề, trước tiên ta hãy xét sự cân bằng của hai vật: một hình hộp chữ nhật có mặt đáy vuông và một hình trụ tròn đứng (Hình 60a). Giả sử hình hộp và hình trụ có cùng chiều cao H và có diện tích đáy S bằng nhau. Trong trường hợp này, trọng tâm của hai vật có cùng độ cao và, ngoài ra, chúng có diện tích mặt đế bằng nhau. Tuy nhiên, mức độ bền của chúng là khác nhau. Số đo mức độ bền của một trạng thái cân bằng nhất định là năng lượng phải tiêu hao để làm nhiễu vĩnh viễn trạng thái đó của vật.
HS B: Thầy muốn nói gì với từ “vĩnh viễn”?
GV: Nghĩa là nếu vật bị lệch đi chút ít, nó không thể trở lại trạng thái ban đầu nữa. Lượng năng lượng này bằng với tích của trọng lượng của vật và độ cao mà trọng tâm phải nâng lên để cho vật không thể trở lại vị trí ban đầu của nó.
Như vậy, trong hai vật được xét, cân bằng của hình trụ là bền hơn.
Bây giờ tôi đề nghị chúng ta quay lại với ví dụ hai vị trí của viên gạch.
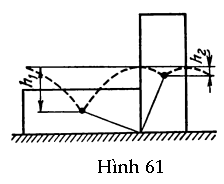
HS A: Nếu chúng ta lật viên gạch, nó sẽ chuyển từ vị trí cân bằng này sang vị trí cân bằng kia. Đường đứt nét trong Hình 61 thể hiện quỹ đạo mô tả bởi trọng tâm của nó trong quá trình này. Để làm thay đổi vị trí của một viên gạch nằm, trọng tâm của nó phải được nâng lên độ cao h1, tiêu hao một năng lượng bằng mgh1, và để làm thay đổi vị trí viên gạch đứng, trọng tâm phải được nâng lên h2, năng lượng tiêu hao là mgh2. Mức độ cân bằng cao hơn của viên gạch nằm là do thực tế
mgh1 > mgh2 (82)
GV: Ít nhất thì em đã thành công trong việc lí giải mức cân bằng cao hơn của vị trí nằm của một vật.
HS B: Nhưng rõ ràng các độ cao h1 và h2 phụ thuộc vào độ cao của trọng tâm phía trên sàn đỡ và vào diện tích của mặt đế. Phải chăng điều đó có nghĩa là khi nói về mức cân bằng của các vật, ta nên so sánh độ cao của trọng tâm và diện tích của mặt đế?
GV: Ừm, nhưng chỉ với trường hợp những đại lượng này ảnh hưởng đến sự chênh lệch độ cao h1 và h2. Như vậy, trong ví dụ với hình hộp và hình trụ, sự so sánh độ cao trọng tâm và diện tích mặt đế là bằng chứng không đủ để xác định xem vật nào bền hơn. Nhân tiện, tôi muốn hướng sự chú ý của các em sang vấn đề sau. Cho đến đây, chúng ta đã ngầm giả sử rằng hai vật trên làm bằng chất liệu giống nhau. Trong trường hợp này, bất đẳng thức (82) có thể được thỏa mãn bởi sự quan sát hình học h1 > h2. Tuy nhiên, trong trường hợp tổng quát, các vật có thể làm bằng những chất liệu khác nhau, và bất đẳng thức (82) có thể được thỏa mãn ngay cả khi h1 < h2 do tỉ trọng khác nhau của các vật. Ví dụ, một viên gạch bần ở vị trí nằm sẽ kém bền hơn hơn một viên gạch chì ở vị trí đứng. Bây giờ chúng ta hãy xét các điều kiện cho sự cân bằng của các vật mà các em biết.
HS A: Tổng của tất cả các lực tác dụng lên một vật phải bằng không. Ngoài ra, vector trọng lực của vật phải rơi vào trong mặt đế của nó.
GV: Tốt. Tuy nhiên, tốt hơn chúng ta nên xét các điều kiện cân bằng ở một dạng khác, khái quát hơn và tiện lợi hơn cho sự áp dụng thực tiễn. Ta nên phân biệt rõ hai điều kiện của sự cân bằng.
Điều kiện thứ nhất: Hình chiếu của tất cả các lực tác dụng lên vật trên một phương bất kì sẽ triệt tiêu lẫn nhau. Nói cách khác, tổng đại số của hình chiếu của tất cả các lực trên một phương bất kì phải bằng không. Điều kiện này cho phép viết nhiều phương trình khi có những phương độc lập trong bài toán: một phương trình cho bài toán một chiều, hai phương trình cho bài toán hai chiều, và ba phương trình cho trường hợp tổng quát (chọn ba phương vuông góc lẫn nhau).
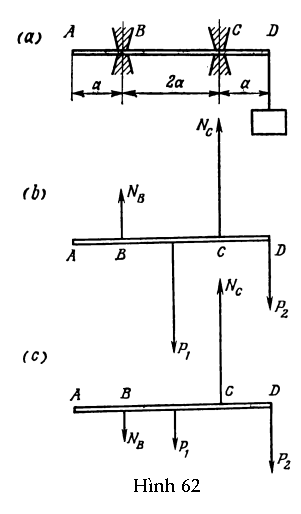
Điều kiện thứ hai (điều kiện moment): Tổng đại số của tất cả các moment lực đối với một trục quay bất kì phải bằng không. Ở đây, tất cả các moment có xu hướng làm quay vật theo một chiều nhất định (ví dụ chiều kim đồng hồ) được lấy dấu cộng và toàn bộ những moment lực làm vật quay theo chiều ngược lại (ngược chiều kim đồng hồ) thì nhận dấu trừ. Để xác lập điều kiện moment, ta làm như sau: (a) xác định tất cả các lực tác dụng lên vật; (b) chọn một điểm nào đó để xét các moment lực; (c) tìm moment của tất cả các lực đối với điểm đã chọn; (d) viết phương trình tổng đại số của các moment, cho nó bằng không. Khi áp dụng điều kiện moment, nên nhớ trong đầu điều sau đây: (1) điều kiện vừa phát biểu áp dụng cho trường hợp khi tất cả các lực trong bài toán và những cánh tay đòn của chúng nằm trong cùng một mặt phẳng (bài toán không phải là ba chiều); và (2) tổng đại số của tất cả các moment phải bằng không đối với một điểm bất kì, hoặc nằm bên trong hoặc nằm bên ngoài vật. Nên nhấn mạnh rằng mặc dù giá trị của từng moment lực thật sự phụ thuộc vào sự chọn lựa điểm (để xét moment lực đối với nó), nhưng trong mọi trường hợp tổng đại số của các moment là bằng không. Để hiểu rõ hơn các điều kiện của sự cân bằng, chúng ta sẽ xét một bài toán đặc biệt. Một cái xà trọng lượng P1 được cố định tại B và C (Hình 62a). Tại điểm D, một vật nặng trọng lượng P2 được treo vào xà. Khoảng cách AB = a, BC = 2a và CD = a. Tìm phản lực NB và NC tại hai điểm đỡ. Giả sử hai phản lực đó có phương thẳng đứng.
Như thường lệ, trước tiên hãy chỉ rõ các lực tác dụng lên vật.
HS A: Vật trong bài toán đã cho là cái xà. Có bốn lực tác dụng lên nó: các trọng lượng P1 và P2, và các phản lực NB và NC.
GV: Hãy chỉ rõ những lực này trên hình vẽ.
HS A: Nhưng em không biết các phản lực là hướng lên hay hướng xuống.
GV: Hãy giả sử rằng cả hai phản lực là hướng lên.
HS A: Vâng, đây là hình vẽ của em (Hình 62b). Tiếp theo, em có thể định rõ điều kiện thứ nhất của sự cân bằng bằng cách viết phương trình
NB + NC = P1 + P2
GV: Tôi không phản đối gì với phương trình này. Tuy nhiên, trong bài toán của chúng ta nếu sử dụng điều kiện thứ hai của sự cân bằng (điều kiện moment) thì đơn giản hơn, áp dụng nó trước tiên với điểm B sau đó là với điểm C.
HS A: Được rồi, em sẽ làm như thế. Như vậy, em có thể viết phương trình đối với điểm B
GV: Phương trình (85) luôn luôn có kết quả dương. Điều này có nghĩa là phản lực NC luôn luôn hướng lên trên (như chúng ta đã giả sử). Phương trình (84) cho kết quả dương khi P1 > P2, âm khi P1 < P2, và bằng không khi P1 = P2. Điều này có nghĩa là khi P1 > P2 thì phản lực NB có chiều như chúng ta đã giả sử, tức là hướng lên trên (xem Hình 62b); khi P1 < P2 thì phản lực NB hướng xuống (xem Hình 62c); và khi P1 = P2 thì không có phản lực NB.
Những câu hỏi và bài tập vật lí phổ thông
L. Tarasov và A. Tarasova
Trần Nghiêm dịch
Phần tiếp theo >>
