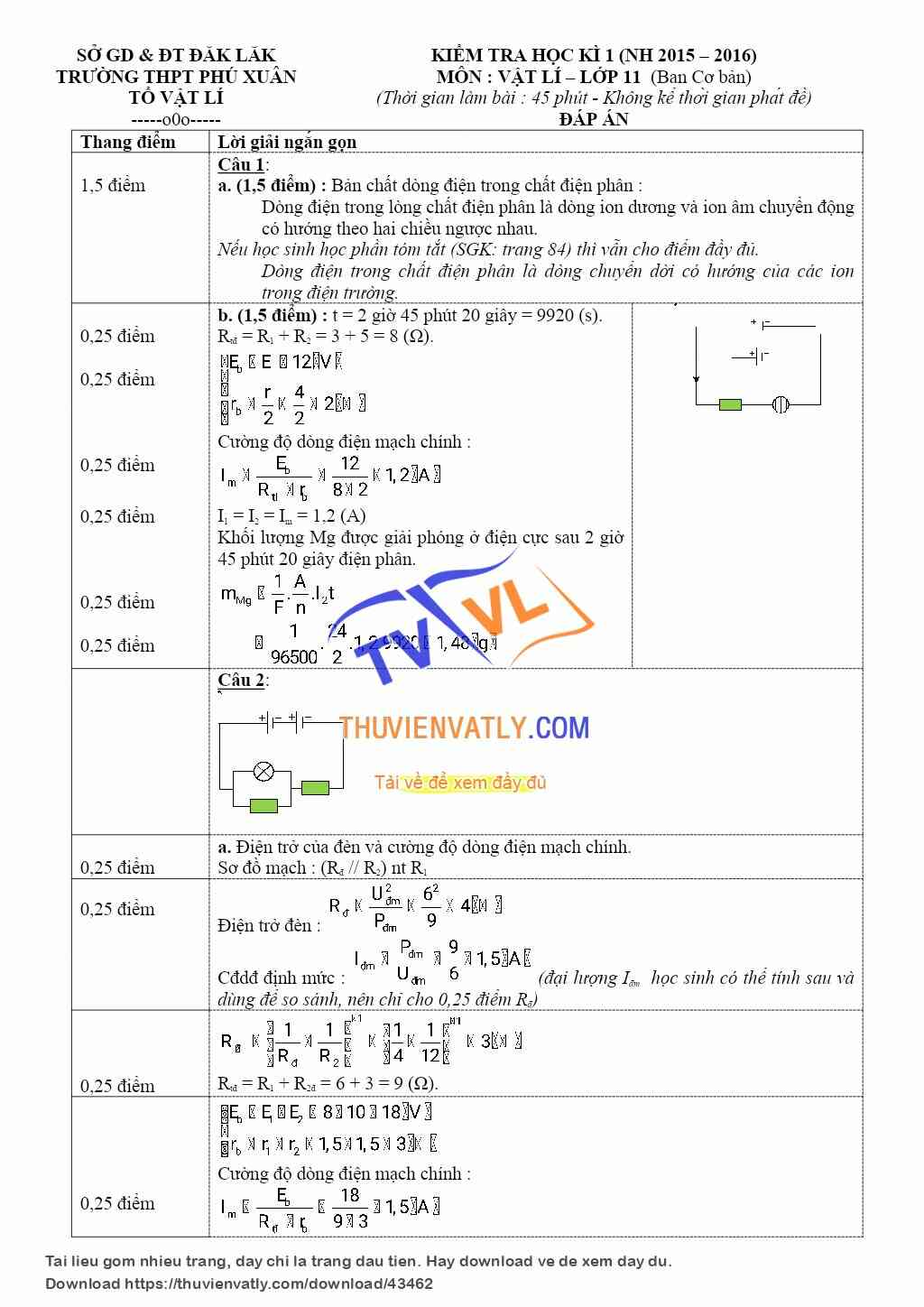
Các tình huống trong Dao động điều hòa.
Vật lí 12. Các dạng bài tập tình huống trong Dao động điều hòa, Sóng cơ và sự truyền sóng cơ cho các bạn HS ôn nhanh phần lý thuyết và bài tập còn yếu
Để download tài liệu Vật lí 12. Các tình huống trong Dao động điều hòa, Sóng cơ và sự truyền sóng cơ các bạn click vào nút TẢI VỀ bên trên.
📁 Chuyên mục: Bài tập tự luận, định tính, tóm tắt lí thuyết Vật lí 12
📅 Ngày tải lên: 13/05/2019
📥 Tên file: 2014-book-ly-thuyet-vat-li-12---ch-1-2-3-20140722-5.thuvienvatly.com.163b1.50143.docx (11.5 MB)
🔑 Chủ đề: dao dong Cac tinh huong Dao dong dieu hoa
Thử sức các bài tập này nhé:
Câu 1:
Một vật dao động điều hoà dọc theo trục Ox với phương trình: . Nếu chọn gốc toạ độ O tại vị trí cân bằng của vật thì gốc thời gian t=0 là lúc vật:
- (A) Qua vị trí cân bằng O theo chiều dương của trục Ox
- (B) Ở vị trí li độ cực đại thuộc phần âm của trục Ox
- (C) Qua vị trí cân bằng O ngược chiều dương của trục Ox
- (D) Ở vị trí li độ cực đại thuộc phần dương của trục Ox
Câu 2:
Một chất điểm dao động điều hoà với phương trình dạng .Lấy , biểu thức gia tốc tức thời của chất điểm là:
- (A)
- (B)
- (C)
- (D)
Câu 3:
Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là
- (A) 0,05 s.
- (B) 0,12 s.
- (C) 0,1 s.
- (D) 0,06 s.
![Tổng hợp công thức vật lý 12 [Chi tiết + Thi tốt nghiệp + Đại học]](https://thuvienvatly.com/home/images/download_thumb/1KG7wUbfWon1PGv_Uyj6zsQN7tcalzZTy.jpg)
