Kính chào các thầy cô và các bạn!
Ở phần từ trường của nhiều dòng điện, khi em làm dạng bài tập về tìm vị trí (hay quỹ tích) của các điểm để từ trường tổng hợp gây ra bởi hai dòng điện [tex]I_{1}, I_{2}[/tex] bằng không. Đối với hai dòng điện ngược chiều [tex]I_{1}, I_{2}[/tex] thì có hai trường hợp: điểm M ([tex]{\vec B_M} = \vec 0\[/tex]) nằm ngoài [tex]{I_1}{I_2}[/tex] về phía [tex]{I_1}[/tex] hoặc về phía [tex]{I_2}[/tex]. Khi giải thì không giải cả hai trường hợp này mà dùng công thức [tex]\frac{{{I_1}}}{{{r_1}}} = \frac{{{I_2}}}{{{r_2}}}[/tex] biện luận về khoảng cách [tex]{r_1},{r_2}[/tex] và loại đi một trường hợp ( loại phía [tex]{I_1}[/tex] hoặc [tex]{I_2}[/tex]) và giải một phương trình của trường hợp còn lại là ra nghiệm của bài toán.
Còn với ba dòng điện [tex]{I_1},{I_2},{I_3}[/tex] thì em không biết cách nào để loại các trường hợp. Cụ thể:
Đề bài: Ba dây dẫn thẳng song song dài vô hạn cùng nằm trong mặt phẳng, hai dây dẫn liên tiếp cách nhau đoạn a = 6 cm, cường độ dòng điện [tex]{I_1} = {I_2} = I, {I_3} = 2I[/tex]. Dây dẫn có dòng điện [tex]{I_3}[/tex] nằm ngoài hai dây dẫn [tex]{I_1},{I_2}[/tex] và dòng điện [tex]{I_3}[/tex] ngược chiều với [tex]{I_1},{I_2}[/tex]. Tìm vị trí của điểm O tại đó cảm ứng từ tổng hợp bằng không?
Bài này là một bài tập trong sách Giải toán vật lí, khi em giải thì vẽ hình ra rồi biễu diễn. Để cảm ứng từ tại điểm đó bằng không thì điểm đó phải thõa mãn: [tex]{{\vec B}_O} = {{\vec B}_1} + {{\vec B}_2} + {{\vec B}_3} = \vec 0\[/tex] và em cũng chia ra 4 trường hợp như hình vẽ
Hình vẽ:
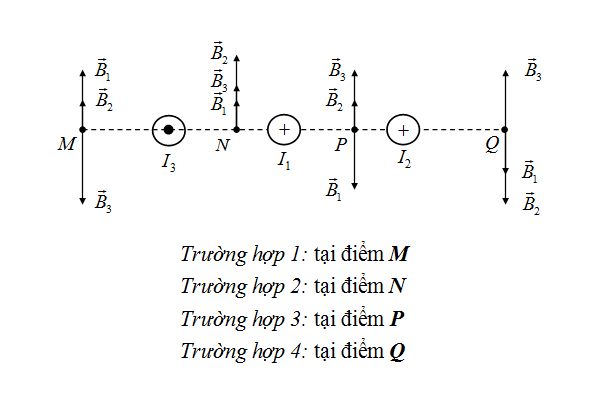
Trong đó trường hợp 2 bị loại đầu tiên. Nhưng nếu giải cả ba phương trình ở ba trường hợp còn lại thì lâu quá và cách giải lại dài nữa.
Mong các bạn và quý thầy cô giúp em có cách nào biện luận loại đi các trường hợp 1 và TH 4 không?. Nếu biện luận được như vậy thì khi giải bài này ta chỉ cần giải phương trình ở trường hợp 3 là được, không cần giải các phương trình ở trường hợp 1 và 4 => bài giải sẽ ngắn gọn hơn nhiều
Tóm lại: mong các bạn và các thầy cô giúp em cách biện luận để loại đi trường hợp 1 và 4, chỉ còn lại trường hợp 3 thõa mãn.
Em xin cảm ơn các thầy cô và bạn nhiều, mong các thầy cô và các bạn giúp đỡ.

