cho tứ diện ABCD có AC=AD=[tex]a\sqrt{2}[/tex] , BC=BD=a, khoảng cách từ B đến (ACD) là [tex]\frac{a}{\sqrt{3}}[/tex]. tính góc giữa hai mặt phẳng (ACD) và (BCD). Biết thể tích khối diện ABCD là [tex]\frac{a^{3}\sqrt{15}}{27}[/tex]
Mong mọi người giúp em với ạ!
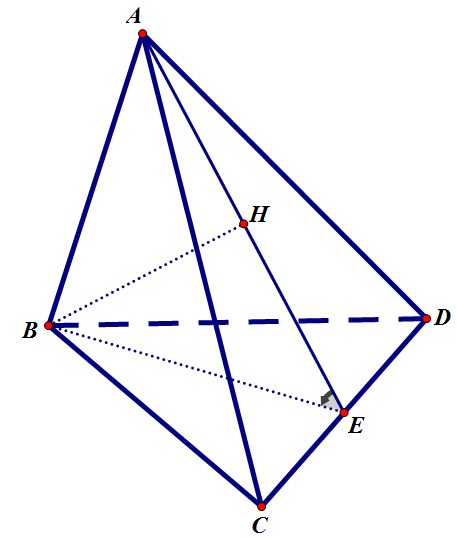
Từ [tex]B[/tex] kẻ [tex]BH\perp AE\,\,\left(H\in AE\right)\Rightarrow BH=\dfrac{a}{\sqrt{3}}[/tex]
Ta có: [tex]V_{ABCD}=\dfrac{1}{3}BH\times S_{ACD}\Leftrightarrow \dfrac{a^3\sqrt{15}}{27}=\dfrac{a\sqrt{3}}{9}\times AE\,.DE\Rightarrow AE^2\,.DE^2=\dfrac{5a^4}{9}\,\,(1)[/tex]
Lại có [tex]\Delta AED[/tex] vuông tại [tex]E\Rightarrow AE^2+DE^2=2a^2\,\,(2)[/tex]
Từ [tex](1)[/tex] và [tex](2)[/tex] suy ra [tex]\left[\begin{array}{l}\left[\begin{array}{l}AE^2=\dfrac{5a^2}{3}\\DE^2=\dfrac{a^2}{3}\end{array}\right.\,\,\,\,\,(I)\\\left[\begin{array}{l}AE^2=\dfrac{a^2}{3}\\DE^2=\dfrac{5a^2}{3}\end{array}\right.\,\,\,\,\,(II)\end{array}\right.[/tex]
[tex]\bullet[/tex] Giải [tex](I):[/tex] [tex]\Delta BED[/tex] vuông tại [tex]D\Rightarrow BE=\sqrt{BD^2-DE^2}=\dfrac{a\sqrt{6}}{3}[/tex]
[tex]\Delta BHE[/tex] vuông tại [tex]H\Rightarrow \sin BEH=\dfrac{BH}{BE}=\dfrac{\sqrt{2}}{2}\Rightarrow \widehat{BEH}=45^o[/tex] suy ra góc giữa hai mặt phẳng [tex]\left(ACD\right)[/tex] và [tex]\left(BCD\right)[/tex] là [tex]45^o.[/tex]
[tex]\bullet[/tex] Giải [tex](II):[/tex] Ta có: [tex]DE=\dfrac{a\sqrt{15}}{3}=\dfrac{CD}{2}>\dfrac{BC+CD}{2}=a\Rightarrow[/tex] vô lý.
