Một con lắc lò xo gồm lò xo nhẹ có độ cứng $k = 100{\rm{\;N}}/{\rm{m}}$ , đầu trên cố định, đầu dưới gắn với vật ${m_1}$ có khối lượng $100{\rm{\;g}}$

Question

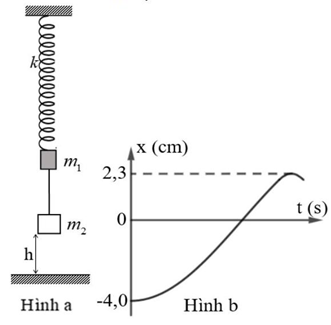
Một con lắc lò xo gồm lò xo nhẹ có độ cứng  $k = 100{\rm{\;N}}/{\rm{m}}$  , đầu trên cố định, đầu dưới gắn với vật  ${m_1}$   có khối lượng  $100{\rm{\;g}}$  , vật  ${m_2}$   có khối lượng  $300{\rm{\;g}}$   nối với  ${m_1}$   bằng một sợi dây mềm, nhẹ, không dãn (Hình  ${\rm{a}}$  ). Ban đầu giữ vật  ${m_1}$    ở vị trí lò xo không biến dạng, khi đó  ${m_2}$   cách mặt đất một khoảng h. Bỏ qua lực cản không khí, lấy  $g = 10{\rm{\;m}}/{{\rm{s}}^2},{\pi ^2} = 10$  . Thả nhẹ vật  ${m_1}$   thì đồ thị li độ theo thời gian của  ${m_1}$    ở khoảng thời gian đầu như hình  $b$  . Giá trị của độ cao  $h$   bằng

Nguyễn Văn Thành · Accepted Answer

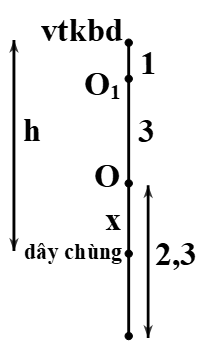
$6,0{\rm{\;cm}}$ Cách 1: Lớp 12. . GĐ1: Cả 2 vật cùng dao động điều hòa đến khi m2 chạm đất. . $A = \Delta {l_0} = \frac{{\left( {{m_1} + {m_2}} \right)g}}{k} = \frac{{\left( {0,1 + 0,3} \right).10}}{{100}} = 0,04m = 4cm$. . $\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} = \sqrt {\frac{{100}}{{0,1 + 0,3}}} = 5\sqrt {10} $   (rad/s). . GĐ2: Dây chùng, m­­1 dao động với vị trí cân bằng mới O1 ­dãn. . $\Delta {l_1} = \frac{{{m_1}g}}{k} = \frac{{0,1.10}}{{100}} = 0,01m = 1cm$. . ${\omega _1} = \sqrt {\frac{k}{{{m_1}}}} = \sqrt {\frac{{100}}{{0,1}}} = 10\sqrt {10} $   (rad/s). . $v = {v_1} \Rightarrow \omega \sqrt {{A^2} - {x^2}} = {\omega _1}\sqrt {A_1^2 - x_1^2} \Rightarrow 5\sqrt {10} .\sqrt {{4^2} - {x^2}} = 10\sqrt {10} .\sqrt {{{\left( {2,3 + 3} \right)}^2} - {{\left( {x + 3} \right)}^2}} $. . $ \Rightarrow x \approx 2cm \Rightarrow h = 4 + x = 6cm$  .. . Cách 2: Lớp 10. . ốc thế năng tại vị trí lò xo không biến dạng. . Bảo toàn cơ năng cho hệ vật từ vị trí lò xo không biến dạng đến khi  ${m_2}$   chạm đất (dây chùng). . $0 = \frac{1}{2}k{h^2} + \frac{1}{2}\left( {{m_1} + {m_2}} \right){v^2} - \left( {{m_1} + {m_2}} \right)gh \Rightarrow \frac{1}{2}\left( {{m_1} + {m_2}} \right){v^2} = \left( {{m_1} + {m_2}} \right)gh - \frac{1}{2}k{h^2}$   (1). . Bảo toàn cơ năng cho vật m1 từ khi m2 chạm đất (dây chùng) đến khi m­­1 xuống vị trí thấp nhất. . $\frac{1}{2}k{h^2} + \frac{1}{2}{m_1}{v^2} - {m_1}gh = \frac{1}{2}k{s^2} - {m_1}gs \Rightarrow \frac{1}{2}{m_1}{v^2} = {m_1}g\left( {h - s} \right) + \frac{1}{2}k\left( {{s^2} - {h^2}} \right)$   (2). . Quãng đường vật m­1 đi từ vị trí lò xo không biến dạng đến vị trí thấp nhất là. . $s = 4 + 2,3 = 6,3cm = 0,063m$. . Lấy  $\frac{{\left( 1 \right)}}{{\left( 2 \right)}} \Rightarrow \frac{{{m_1} + {m_2}}}{{{m_1}}} = \frac{{\left( {{m_1} + {m_2}} \right)gh - \frac{1}{2}k{h^2}}}{{{m_1}g\left( {h - s} \right) + \frac{1}{2}k\left( {{s^2} - {h^2}} \right)}}$. . $ \Rightarrow \frac{{0,1 + 0,3}}{{0,1}} = \frac{{\left( {0,1 + 0,3} \right).10.h - \frac{1}{2}.100.{h^2}}}{{0,1.10.\left( {h - 0,063} \right) + \frac{1}{2}.100.\left( {0,{{063}^2} - {h^2}} \right)}} \Rightarrow h \approx 0,06m = 6cm$

Một con lắc lò xo gồm lò xo nhẹ có độ cứng $k = 100{\rm{\;N}}/{\rm{m}}$ , đầu trên cố định, đầu dưới gắn với vật ${m_1}$ có khối lượng $100{\rm{\;g}}$

Câu hỏi

Câu trả lời hay nhất

Câu trước | Câu kế tiếp

Các câu trả lời

Sách Chinh Phục Kì Thi Vào 10 Chuyên Môn Vật Lí

Sách Chuyên Đề Bồi Dưỡng Học Sinh Giỏi Vật Lý 8

Làm thêm Trắc nghiệm ôn thi THPT

Một đoạn mạch điện xoay chiều gồm điện trở thuần R mắc nối tiếp với tụ điện C. Nếu dung kháng ZC bằng R thì cường độ dòng điện chạy qua điện trở luôn

Số nucleon trong hạt nhân $_{82}^{206}\;{\rm{Pb}}$ là

Một khung dây hình chữ nhật có chiều dài 25 cm, được đặt vuông góc với các đường sức từ của một từ trường đều có cảm ứng từ B=4.10-3 T. Từ thông gửi qua

Trong thí nghiệm giao thoa sóng ở mặt nước, 2 nguồn kết hợp A và B dao động cùng pha. Hai điểm M, N nằm trên đoạn AB là 2 điểm dao động cực đại lần lượt

Xét chuyển động ném ngang của một chất điểm M có gốc tọa độ O tại vị trị ném và hệ trục tọa độ Oxy (Ox nằm ngang; Oy đứng thẳng) nằm trong mặt phẳng quỹ

Một vật dao động điều hòa trên trục Ox quanh vị trí cân bằng O . Gọi A, ω và φ lần lượt là biên độ, tần số góc và pha ban đầu của dao động. Biểu thức

Một con lắc lò xo gồm lò xo nhẹ có độ cứng k=100N/mk = 100{\rm{\;N}}/{\rm{m}} , đầu trên cố định, đầu dưới gắn với vật m1{m_1} có khối lượng 100g100{\rm{\;g}}

Câu hỏi

Câu trả lời hay nhất

Câu trước | Câu kế tiếp

Các câu trả lời

Sách Chinh Phục Kì Thi Vào 10 Chuyên Môn Vật Lí

Sách Chuyên Đề Bồi Dưỡng Học Sinh Giỏi Vật Lý 8

Làm thêm Trắc nghiệm ôn thi THPT

Một đoạn mạch điện xoay chiều gồm điện trở thuần R mắc nối tiếp với tụ điện C. Nếu dung kháng ZC bằng R thì cường độ dòng điện chạy qua điện trở luôn

Số nucleon trong hạt nhân 20682Pb_{82}^{206}\;{\rm{Pb}} là

Một khung dây hình chữ nhật có chiều dài 25 cm, được đặt vuông góc với các đường sức từ của một từ trường đều có cảm ứng từ B=4.10-3 T. Từ thông gửi qua

Trong thí nghiệm giao thoa sóng ở mặt nước, 2 nguồn kết hợp A và B dao động cùng pha. Hai điểm M, N nằm trên đoạn AB là 2 điểm dao động cực đại lần lượt

Xét chuyển động ném ngang của một chất điểm M có gốc tọa độ O tại vị trị ném và hệ trục tọa độ Oxy (Ox nằm ngang; Oy đứng thẳng) nằm trong mặt phẳng quỹ

Một vật dao động điều hòa trên trục Ox quanh vị trí cân bằng O . Gọi A, ω và φ lần lượt là biên độ, tần số góc và pha ban đầu của dao động. Biểu thức

Một con lắc lò xo gồm lò xo nhẹ có độ cứng $k = 100{\rm{\;N}}/{\rm{m}}$ , đầu trên cố định, đầu dưới gắn với vật ${m_1}$ có khối lượng $100{\rm{\;g}}$

Số nucleon trong hạt nhân $_{82}^{206}\;{\rm{Pb}}$ là