Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.
Câu hỏi
🗣️ Trần Thị Nhật hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
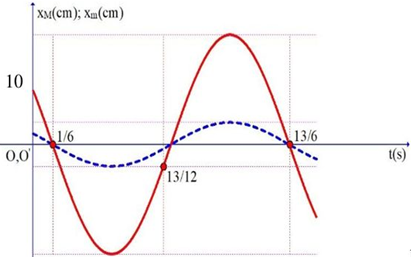
Một con lắc lò xo dao động trên phương ngang không ma sát, vật nặng có khối lượng \(m\), lò xo có độ cứng \(k\), trên lò xo có một điểm \(M\). Khi vật m dao động điều hòa quanh vị trí cân bằng \(O\) thì \(M\) trên lò xo cũng dao động quanh vị trí cân bằng O’. Đồ thị sự phụ thuộc của li độ theo thời gian của \(m\) và \(M\) quanh \(O\) và \(O\)' như hình vẽ. Tại thời điểm \(t = \frac{2}{3}\;s\) thì điểm \(M\) được giữ cố định, khi đó vật \(m\) sẽ dao động với biên độ gần nhất với giá trị nào sau đây?
(A) \(15\;cm\) .
(B) \(16\;cm\) .
(C) \(18\;cm\) .
(D) \(17\;cm\) .
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: ,2023, de thi thu vat li so ha tinh lan 2 co dap an.
Câu trả lời hay nhất
🕵 Bạn Nguyễn Ngọc Đức trả lời:
Chọn câu (A): \(15\;cm\) .
Đáp án: A \[T = \frac{{13}}{6} - \frac{1}{6} = 2s \to \omega = \frac{{2\pi }}{T} = \pi ({\rm{rad}}/{\rm{s}})\] \[{x_m} = {A_m}\cos \left[ {\pi \left( {t - \frac{1}{6}} \right) + \frac{\pi }{2}} \right] = {A_m}\cos \left( {\pi t + \frac{\pi }{3}} \right)\] Tại t = 0 thì \[10 = {A_m}\cos \left( {\pi \cdot 0 + \frac{\pi }{3}} \right) \Rightarrow {A_m} = 20\;{\rm{cm}}\] Tại \[t = \frac{{13}}{{12}}s\] thì - \[{A_M} = 20\cos \left( {\pi \cdot \frac{{13}}{{12}} + \frac{\pi }{3}} \right)\]\[ \Rightarrow {A_M} = 5\sqrt 6 - 5\sqrt 2 \;{\rm{cm}}\] Tại \[t = \frac{2}{3}s\] thì \[{x_m} = {A_m}\cos \left( {\pi \frac{2}{3} + \frac{\pi }{3}} \right) = - {A_m} \Rightarrow {x_M} = - {A_M}\] (M cùng pha với m) Giữ cố định điểm M thì vị trí cân bằng dịch sang trái một đoạn bằng \(\left| {{x_M}} \right| = {A_M}\) Biên độ của vật m lúc sau là \({A_m} - {A_M} = 20 - (5\sqrt 6 - 5\sqrt 2 ) \approx 14,824\;{\rm{cm}}\)
![Đáp án: A
\[T = \frac{{13}}{6} - \frac{1}{6} = 2s \to \omega = \frac{{2\pi }}{T} = \pi ({\rm{rad}}/{\rm{s}})\]
\[{x_m} = {A_m}\cos \left[ {\pi \left( {t - \frac{1}{6}} \right) + \frac{\pi }{2}} \right] = {A_m}\cos \left( {\pi t + \frac{\pi }{3}} \right)\]
Tại t = 0 thì \[10 = {A_m}\cos \left( {\pi \cdot 0 + \frac{\pi }{3}} \right) \Rightarrow {A_m} = 20\;{\rm{cm}}\]
Tại \[t = \frac{{13}}{{12}}s\] thì - \[{A_M} = 20\cos \left( {\pi \cdot \frac{{13}}{{12}} + \frac{\pi }{3}} \right)\]\[ \Rightarrow {A_M} = 5\sqrt 6 - 5\sqrt 2 \;{\rm{cm}}\]
Tại \[t = \frac{2}{3}s\] thì \[{x_m} = {A_m}\cos \left( {\pi \frac{2}{3} + \frac{\pi }{3}} \right) = - {A_m} \Rightarrow {x_M} = - {A_M}\] (M cùng pha với m) Giữ cố định điểm M thì vị trí cân bằng dịch sang trái một đoạn bằng \(\left| {{x_M}} \right| = {A_M}\)
Biên độ của vật m lúc sau là \({A_m} - {A_M} = 20 - (5\sqrt 6 - 5\sqrt 2 ) \approx 14,824\;{\rm{cm}}\)](/images/cau-hoi-2/tra-loi-mot-con-lac-lo-xo-dao-dong-tren-phuong-ngang-khong-0-41337.png)
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Phạm Văn Hiệp viết:
Chọn C, \(18\;cm\) .
👤 Trần Văn Đông viết:
Chọn D, \(17\;cm\) .
👤 Lê Văn Đại viết:
Chọn B, \(16\;cm\) .
👤 Trần Văn Lợi viết:
Chọn A, \(15\;cm\) .
➥ 🗣️ Trần Thị Nhật trả lời: Cảm ơn bạn, câu này hình như có trong file doc này (2023) Đề thi thử Vật Lí Sở Hà Tĩnh Lần 2 có đáp án
👤 Bùi Văn Phú viết:
Chọn A: \(15\;cm\) .
Gửi bạn các file hữu ích đi kèm câu hỏi:
- (2023) Đề thi thử Vật Lí Sở Hà Tĩnh Lần 2 có đáp án (.doc)
- (2023) Đề thi thử Vật Lí Sở Hà Tĩnh Lần 1 có đáp án (.doc)
- (2023) Đề thi thử Vật Lí THPT Kỳ Anh - Hà Tĩnh (Lần 1) có đáp án (.doc)
- (2023) Đề thi thử Vật lí Sở giáo dục và đào tạo Hà Tĩnh (Lần 3) có đáp án (.doc)
- (2023) Đề thi thử Vật Lí Sở GD Hà Tĩnh có đáp án (.doc)
- (2023) Đề thi thử Vật Lí THPT Dĩ An - Bình Dương (Lần 1) có đáp án (.doc)
- Có khả năng Ngân hà là một lỗ sâu đục khổng lồ
- [Ảnh] Một cái lỗ trên sao Hỏa
