Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.
Câu hỏi
🗣️ Trần Thị Nguyên hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
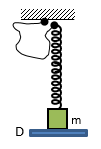
Cho cơ hệ như hình vẽ: lò xo rất nhẹ có độ cứng 100 N/m nối với vật m có khối lượng 1 kg , sợi dây rất nhẹ có chiều dài 2,5 cm và không giãn, một đầu sợi dây nối với lò xo, đầu còn lại nối với giá treo cố định. Vật m được đặt trên giá đỡ D và lò xo không biến dạng, lò xo luôn có phương thẳng đứng, đầu trên của lò xo lúc đầu sát với giá treo. Cho giá đỡ D bắt đầu chuyển động thẳng đứng xuống dưới nhanh dần đều với gia tốc có độ lớn là 5 m/s2. Bỏ qua mọi lực cản, lấy g = 10 m/s2. Xác định thời gian ngắn nhất từ khi m rời giá đỡ D cho đến khi vật m trở lại vị trí lò xo không biến dạng lần thứ nhất.
(A) A . \[\frac{\pi }{3}s\]
(B) B . \[\frac{\pi }{5}s\]
(C) C . \[\frac{\pi }{6}s\]
(D) D . \[\frac{{5\pi }}{6}s\]
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: ,2023, de thi thu vat li thpt tran cao van co dap an.
Câu trả lời hay nhất
🕵 Bạn Phạm Ngọc Nam trả lời:
Chọn câu (C): C . \[\frac{\pi }{6}s\]
c Giả sử m bắt đầu rời khỏi giá đỡ D khi lò xo dãn 1 đoạn là Δ l, Tại vị trí này ta có \(mg - k\Delta \ell = ma = > \Delta \ell = \frac{{m(g - a)}}{k} = 5(cm)\) Lúc này vật đã đi được quãng đường S = 2,5+5=7,5(cm) Mặt khác quãng đường \(S = \frac{{a.{t^2}}}{2} = > t = \sqrt {\frac{{2S}}{a}} = \,\sqrt {\frac{{2.7,5}}{{500}}} = \frac{{\sqrt 3 }}{{10}}(s)\) Tại vị trí này vận tốc của vật là: v=a.t = \[50\sqrt 3 \] (cm/s) Độ biến dạng của lò xo khi vật ở vị trí cân bằng là: \(\Delta {\ell _0} = \frac{{m.g}}{k} = > \Delta {\ell _0} = 10(cm)\) => li độ của m tại vị trí rời giá đỡ x = - 5(cm). Tần số góc dao động : \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{100}}{1}} = 10rad/s.\) Biên độ dao động của vật m ngay khi rời giá D là: \(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{5^2} + {{(\frac{{50\sqrt 3 }}{{10}})}^2}} = 10\;cm\) Lưu ý : Biên độ : \(A = \Delta {\ell _0} = 10(cm).\) chu kì: \[T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{10}} = \frac{\pi }{5}s.\] T hời gian ngắn nhất từ khi m rời giá đỡ D cho đến khi vật m trở lại vị trí lò xo không biến dạng lần thứ nhất. (Dùng vòng tròn pha ) \[t = \frac{T}{{12}} + \frac{T}{2} + \frac{T}{4} = \frac{{5T}}{6} = \frac{\pi }{6}s.\] => đáp án C.
![c Giả sử m bắt đầu rời khỏi giá đỡ D khi lò xo dãn 1 đoạn là Δ l,
Tại vị trí này ta có \(mg - k\Delta \ell = ma = > \Delta \ell = \frac{{m(g - a)}}{k} = 5(cm)\)
Lúc này vật đã đi được quãng đường S = 2,5+5=7,5(cm)
Mặt khác quãng đường \(S = \frac{{a.{t^2}}}{2} = > t = \sqrt {\frac{{2S}}{a}} = \,\sqrt {\frac{{2.7,5}}{{500}}} = \frac{{\sqrt 3 }}{{10}}(s)\)
Tại vị trí này vận tốc của vật là: v=a.t = \[50\sqrt 3 \] (cm/s)
Độ biến dạng của lò xo khi vật ở vị trí cân bằng là:
\(\Delta {\ell _0} = \frac{{m.g}}{k} = > \Delta {\ell _0} = 10(cm)\)
=> li độ của m tại vị trí rời giá đỡ
x = - 5(cm).
Tần số góc dao động :
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{100}}{1}} = 10rad/s.\)
Biên độ dao động
của vật m ngay khi rời giá D là:
\(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{5^2} + {{(\frac{{50\sqrt 3 }}{{10}})}^2}} = 10\;cm\)
Lưu ý : Biên độ : \(A = \Delta {\ell _0} = 10(cm).\)
chu kì: \[T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{10}} = \frac{\pi }{5}s.\]
T hời gian ngắn nhất từ khi m rời giá đỡ D cho đến khi
vật m trở lại vị trí lò xo không biến dạng lần thứ nhất.
(Dùng vòng tròn pha ) \[t = \frac{T}{{12}} + \frac{T}{2} + \frac{T}{4} = \frac{{5T}}{6} = \frac{\pi }{6}s.\] => đáp án C.](/images/cau-hoi-5/tra-loi-cho-co-he-nhu-hinh-ve-lo-xo-rat-nhe-co-do-cung-0-13163.png)
![c Giả sử m bắt đầu rời khỏi giá đỡ D khi lò xo dãn 1 đoạn là Δ l,
Tại vị trí này ta có \(mg - k\Delta \ell = ma = > \Delta \ell = \frac{{m(g - a)}}{k} = 5(cm)\)
Lúc này vật đã đi được quãng đường S = 2,5+5=7,5(cm)
Mặt khác quãng đường \(S = \frac{{a.{t^2}}}{2} = > t = \sqrt {\frac{{2S}}{a}} = \,\sqrt {\frac{{2.7,5}}{{500}}} = \frac{{\sqrt 3 }}{{10}}(s)\)
Tại vị trí này vận tốc của vật là: v=a.t = \[50\sqrt 3 \] (cm/s)
Độ biến dạng của lò xo khi vật ở vị trí cân bằng là:
\(\Delta {\ell _0} = \frac{{m.g}}{k} = > \Delta {\ell _0} = 10(cm)\)
=> li độ của m tại vị trí rời giá đỡ
x = - 5(cm).
Tần số góc dao động :
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{100}}{1}} = 10rad/s.\)
Biên độ dao động
của vật m ngay khi rời giá D là:
\(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{5^2} + {{(\frac{{50\sqrt 3 }}{{10}})}^2}} = 10\;cm\)
Lưu ý : Biên độ : \(A = \Delta {\ell _0} = 10(cm).\)
chu kì: \[T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{10}} = \frac{\pi }{5}s.\]
T hời gian ngắn nhất từ khi m rời giá đỡ D cho đến khi
vật m trở lại vị trí lò xo không biến dạng lần thứ nhất.
(Dùng vòng tròn pha ) \[t = \frac{T}{{12}} + \frac{T}{2} + \frac{T}{4} = \frac{{5T}}{6} = \frac{\pi }{6}s.\] => đáp án C.](/images/cau-hoi-5/tra-loi-cho-co-he-nhu-hinh-ve-lo-xo-rat-nhe-co-do-cung-1-12082.png)
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Lê Văn Thông viết:
Chọn C, C . \[\frac{\pi }{6}s\]
➥ 🗣️ Trần Thị Nguyên trả lời: Cảm ơn bạn, câu này hình như có trong file doc này (2023) Đề thi thử Vật Lí THPT Trần Cao Vân có đáp án
👤 Phạm Văn Khiêm viết:
Chọn D, D . \[\frac{{5\pi }}{6}s\]
👤 Trần Văn Quốc viết:
Chọn B, B . \[\frac{\pi }{5}s\]
👤 Phạm Văn Phương viết:
Chọn A, A . \[\frac{\pi }{3}s\]
👤 Phạm Văn Dũng viết:
Chọn C: C . \[\frac{\pi }{6}s\]
Gửi bạn các file hữu ích đi kèm câu hỏi:
- (2023) Đề thi thử Vật Lí THPT Trần Cao Vân có đáp án (.doc)
- (2023) Đề thi thử Vật lí THPT soạn theo ma trận đề minh họa BGD (Đề 14) có đáp án (.doc)
- (2023) Đề thi thử Vật lí THPT soạn theo ma trận đề minh họa BGD (Đề 16) có đáp án (.doc)
- (2023) Đề thi thử Vật Lí THPT Chuyên Lương Văn Chánh - Phú Yên có đáp án (.doc)
- (2023) Đề thi thử Vật lí THPT soạn theo ma trận đề minh họa BGD (Đề 13) có đáp án (.doc)
- (2023) Đề thi thử Vật lí THPT soạn theo ma trận đề minh họa BGD (Đề 2) có đáp án (.doc)
- Năng lượng và động lượng không bảo toàn đối với vật chất bình thường?
- Mô hình toán học mới cho các lí thuyết không-thời gian
