$P$ và $Q$ là hai điểm trên mặt nước cách nhau một khoảng $20{\rm{\;cm}}$ . Tại một điểm ${\rm{O}}$ trên đường thẳng ${\rm{PQ}}$

Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.

Câu hỏi

🗣️ Nguyễn Văn Dũng hỏi: Cho mình hỏi một câu Vật lý Lớp 11 trong sách bài tập Sách Kết Nối Tri Thức

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: giai sbt vat ly 11 kntt su truyen nang luong cua song co co dap an.

Câu trả lời hay nhất

🕵 Bạn Trần Thị Phú trả lời:

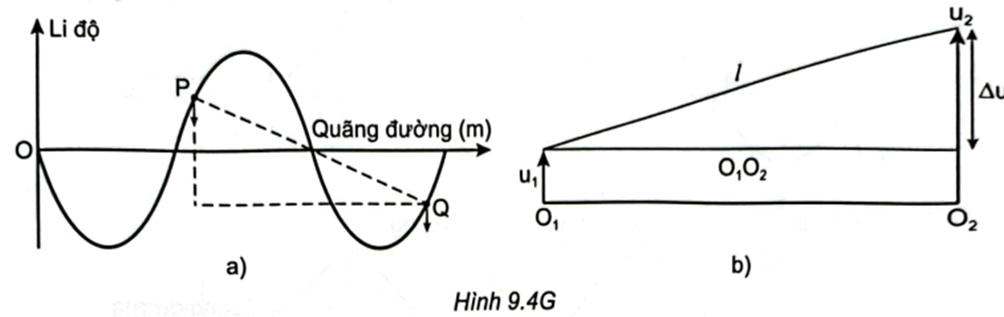
Đối với trường hợp sóng ngang, khoảng cách giữa hai điểm P, Q khi dao động được mô tả như Hình 9.4G. Gọi O1, O2 lần lượt là vị trí cân bằng của P và Q; u1, u2 lần lượt là li độ dao động của các phần tử tại P và Q;${\rm{\Delta }}u = {u_1} - {u_2}$ . Khoảng cách giữa P và Q trong quá trình dao động là: $l = \sqrt {{{\left( {{{\rm{O}}_1}{{\rm{O}}_2}} \right)}^2} + {{({\rm{\Delta u}})}^2}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{l_{{\rm{min}}}} = \sqrt {{{\left( {{{\rm{O}}_1}{{\rm{O}}_2}} \right)}^2} + {{(0)}^2}} = {{\rm{O}}_1}{{\rm{O}}_2}}\\{{l_{{\rm{max}}}} = \sqrt {{{\left( {{{\rm{O}}_1}{{\rm{O}}_2}} \right)}^2} + {{\left( {{\rm{\Delta }}{{\rm{u}}_{{\rm{max}}}}} \right)}^2}} }\end{array}} \right.$ Vậy khoảng cách gần nhất giữa P và Q là: ${l_{{\rm{min}}}} = {O_1}{O_2} = 20{\rm{\;cm}}$ . Khoảng cách xa nhất giữa P và Q là: ${l_{{\rm{max}}}} = \sqrt {{{\left( {{{\rm{O}}_1}{{\rm{O}}_2}} \right)}^2} + {{\left( {{\rm{\Delta }}{{\rm{u}}_{{\rm{max}}}}} \right)}^2}}$ . Giả sử sóng truyền qua P rồi mới đến Q thì dao động tại P sớm pha hơn Q là: ${\rm{\Delta }}\varphi = \frac{{2\pi \left( {PQ} \right)}}{\lambda } = \frac{{8\pi }}{3}$ Chọn mốc thời gian để phương trình dao động của phần tử tại P là: ${u_1} = 5{\rm{cos}}\omega t\left( {{\rm{cm}}} \right)$ thì phương trình dao động của phần tử tại Q là: ${u_2} = 5{\rm{cos}}\left( {\omega t - \frac{{8\pi }}{3}} \right)\left( {{\rm{cm}}} \right)$ . ${\rm{\Delta u}} = {{\rm{u}}_1} - {{\rm{u}}_2} = 5{\rm{cos}}\left( {\omega {\rm{t}} - \frac{{8\pi }}{3}} \right) - 5{\rm{cos}}\omega {\rm{t}} = 5\sqrt 3 {\rm{cos}}\left( {\omega {\rm{t}} - \frac{{5\pi }}{6}} \right)\left( {{\rm{cm}}} \right)$ $\Rightarrow {\rm{\Delta }}{{\rm{u}}_{{\rm{max}}}} = 5\sqrt 3 {\rm{\;cm}}$ . ${l_{{\rm{max}}}} = \sqrt {{{(20)}^2} + {{(5\sqrt 3 )}^2}} = 5\sqrt {19} {\rm{\;cm}}.$

---

Câu trước | Câu kế tiếp

Gửi bạn các file hữu ích đi kèm câu hỏi:

• Giải SBT Vật lý 11 KNTT Sự truyền năng lượng của sóng cơ có đáp án (.doc)
• Giải SGK Vật lí 11 KNTT Bài 9. Sóng ngang. Sóng dọc. Sự truyền năng lượng của sóng cơ có đáp án (.doc)
• Trắc nghiệm Vật lí 11 KNTT Bài 9: Sóng ngang. Sóng dọc. Sự truyền năng lượng của sóng cơ có đáp án (.doc)
• Giải SBT Vật lý 11 KNTT Sự chuyển hoá năng lượng trong dao động điều hoà có đáp án (.doc)
• Trắc nghiệm Lý 11 KNTT Bài 9. Sóng ngang. Sóng dọc. Sự truyền năng lượng của sóng cơ có đáp án (.doc)
• Giải SBT Vật lý 11 KNTT Sóng dừng đáp án (.doc)
• Phát hiện có nước trên một tiểu hành tinh thứ hai
• Phát hiện hơi nước trên một hành tinh đá ở xa