Gian nan con đường ‘phát minh lại’ thuyết lượng tử

Các nhà vật lí đã có một thế kỉ vật lộn với những nghịch lí của thuyết lượng tử. Và nay một số người họ đang cố gắng phát minh lại nó.

Philip Ball (Nature, 11/9/2013)

Nếu sự thật được kể cho đúng, thì chỉ có vài nhà vật lí thật sự từng cảm thấy dễ chịu với thuyết lượng tử. Đã sống với nó trong hơn một thế kỉ qua, họ đã học được cách thích ứng để có một mối quan hệ xuôi chèo mát mái; các nhà vật lí ngày nay thường sử dụng toán học của hành trạng lượng tử để thực hiện những tính toán hết sức chính xác về cấu trúc phân tử, các va chạm hạt năng lượng cao, hành trạng bán dẫn, quang phổ phát xạ, và nhiều thứ khác.

Nhưng các tương tác đó có xu hướng cứng nhắc. Hễ khi các nhà nghiên cứu cố gắng lột bỏ lớp mặt nạ và dấn vào ý nghĩa của cơ sở toán học đó, họ liền vấp phải một bức tường nghịch lí dường như không thể xuyên thủng nổi. Liệu vạn vật có thể thật sự vừa là sóng vừa là hạt hay không? Con mèo Schrödinger có thật sự vừa sống vừa chết hay không? Có đúng là cho dù phép đo tinh vi nhất cũng có thể bằng cách nào đó có tác động đối với những hạt ở xa nửa đường Vũ trụ hay không?

Nhiều nhà vật lí phản ứng với tính lạ lẫm cố hữu này bằng cách xét lại ‘cách hiểu Copenhagen’ đã được thiết lập bởi Niels Bohr, Werner Heisenberg và các đồng sự của họ khi họ xây dựng thuyết lượng tử thành dạng thức hiện đại của nó hồi thập niên 1920. Cách hiểu Copenhagen phát biểu rằng tính lạ lẫm phản ánh những hạn chế căn bản về cái có thể được biết về thế giới, và người ta phải chấp nhận như thế - hay nói theo nhà vật lí David Mermin thuộc trường Đại học Cornell ở Ithaca, New York, là “hãy ngậm miệng lại và tính toán đi!”¹

Nhưng luôn có một số người không chịu ngậm miệng – họ quyết tâm gỡ lớp mặt nạ xuống và tìm hiểu ý nghĩa của thuyết lượng tử. “Gì mà thế giới này buộc chúng ta phải mò mẫm tìm đường đi với sự hỗ trợ của một thực thể trừu tượng như thế?”, câu hỏi được nêu ra ra bởi nhà vật lí Maximilian Schlosshauer thuộc trường Đại học Portland ở Oregon, Mĩ, ông đang ám chỉ tới nguyên lí bất định; hàm sóng mô tả xác suất tìm thấy một hệ ở những trạng thái nhất định; và tất cả những công cụ toán học khác có mặt trong các quyển giáo trình về thuyết lượng tử.

Trong hơn một thập niên qua, một nhóm nhỏ gồm những người thích hỏi như thế này cho rằng cách duy nhất để tiến về phía trước là đánh đổ thực thể trừu tượng đó và bắt đầu xây dựng lại lí thuyết. Họ là một nhóm đa dạng, mỗi người có một quan điểm khác nhau về cách thức “xây dựng lại thuyết lượng tử”. Nhưng họ có chung một niềm tin là các nhà vật lí trong thế kỉ qua đã và đang khảo sát thuyết lượng tử từ một góc độ sai lầm, làm cho cái bóng của nó trông kì cục, ma quái và khó giải mã. Nếu họ tìm thấy một góc nhìn thích hợp, thì họ tin rằng mọi thứ sẽ trở nên sáng tỏ, và những bí ẩn lâu nay như bản chất lượng tử của lực hấp dẫn có thể được giải quyết theo một cách tự nhiên, rõ ràng nào đó – có lẽ là một phương diện của một lí thuyết xác suất khái quát hóa nào đó.

“Nỗ lực căn bản lượng tử nhất hết thảy,” theo lời Christopher Fuchs thuộc Viện Vật lí Lí thuyết Perimeter ở Waterloo, Canada, “sẽ là nỗ lực có thể viết nên một câu chuyện – một câu chuyện theo nghĩa đen, với ngôn từ chất phác – có sức thuyết phục và hình tượng oai nghi đến mức cơ sở toán học của cơ học lượng tử ở mức chi tiết kĩ thuật chính xác của nó tất nhiên không còn trụ vững nữa.”

Ảnh minh họa

Một đề xuất rất hợp lí

Một trong những nỗ lực đầu tiên kể lại một câu chuyện như thế xuất hiện vào năm 2001, khi Lucien Hardy, lúc ấy làm việc tại trường Đại học Oxford ở Anh, đề xuất rằng thuyết lượng tử có thể được suy luận ra từ một tập hợp nhỏ gồm những tiên đề “rất hợp lí” về cách đo các xác suất trong một hệ bất kì², ví dụ như tung một đồng xu trong không khí.

Hardy bắt đầu với việc lưu ý rằng một hệ cổ điển có thể được đặc trưng hoàn toàn bằng cách đo một số lượng nhất định những trạng thái “nguyên chủng”, cái ông kí hiệu là N. Đối với một phép tung đồng xu, trong đó kết quả luôn luôn là sấp hoặc ngửa, thì N bằng 2. Đối với phép lăn xúc xắc, trong đó khối lập phương phải dừng lại với một trong sáu mặt ngửa lên, N bằng 6.

Tuy nhiên, trong thế giới lượng tử, xác suất hoạt động không giống như vậy. Việc đo spin của một electron, chẳng hạn, có thể phân biệt hai trạng thái thuần khiết, chúng có thể được mô tả một cách trực quan là quay theo chiều kim đồng hồ hoặc ngược chiều kim đồng hồ, ví dụ, xung quanh một trục thẳng đứng. Nhưng, không giống như trong thế giới cổ điển, spin của electron là một kết hợp của hai trạng thái lượng tử trước khi phép đo được thực hiện, và kết hợp đó biến thiên theo một thể liên tục. Hardy lí giải điều đó qua một ‘tiên đề tính liên tục’ đòi hỏi các trạng thái thuần khiết chuyển từ dạng này sang dạng kia theo một cách trơn tru. Tiên đề này hóa ra hàm ý rằng cần ít nhất N² phép đo để định rõ hoàn toàn một hệ - một liên hệ tương ứng với bức tranh lượng tử thông thường.

Nhưng, trên nguyên tắc, theo Hardy, tiên đề tính liên tục còn cho phép các lí thuyết bậc cao hơn trong đó một định nghĩa hoàn chỉnh của hệ đòi hỏi N³, N⁴ hoặc nhiều phép đo hơn nữa³, để những sai lệch hết sức nhỏ so với hành trạng lượng tử bình thường có thể được quan sát thấy trong phòng thí nghiệm. Tuy nhiên, ông không cố phân tích những khả năng như thế một cách chi tiết; mục tiêu lớn hơn của ông là chỉ ra vật lí lượng tử có thể được đúc khuôn lại như thế nào dưới dạng một lí thuyết xác suất tổng quát. Có thể hình dung, theo ông, một lí thuyết như vậy có thể được suy luận ra bởi các nhà toán học thế kỉ 19 mà không cần biết tới những động thái mang lối kinh nghiệm đã dẫn Max Planck và Albert Einstein tới chỗ khởi xướng cơ học lượng tử vào đầu thế kỉ 20.

Fuchs cảm thấy hứng khởi từ bài báo của Hardy. “Nó tựa như một nhát búa bổ vào đầu tôi và đã định hình lại suy nghĩ của tôi kể từ đó,” ông nói, và ông tự thuyết phục mình theo đuổi cách tiếp cận xác suất một cách toàn tâm toàn ý.

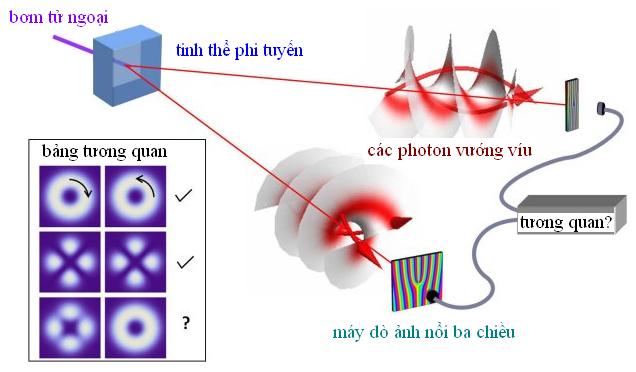
Fuchs đặc biệt hăm hở lí giải khái niệm khó hiểu là sự vướng víu: một tình huống trong đó các trạng thái lượng tử của hai hoặc nhiều hạt là tương thuộc nhau, nghĩa là một phép đo tiến hành trên một hạt sẽ tức thời cho phép người đo xác định trạng thái của hạt kia. Ví dụ, hai photon được phát ra từ một hạt nhân nguyên tử theo hai chiều ngược nhau có thể bị vướng víu sao cho một photon bị phân cực ngang còn photon kia thì phân cực dọc. Trước khi thực hiện bất kì phép đo nào, trạng thái phân cực của hai photon là tương quan nhưng không cố định. Tuy nhiên, một khi tiến hành phép đo trên một photon, thì photon kia cũng tức thời được xác định – cho dù nó đang ở xa nhiều năm ánh sáng.

Như Einstein và các cộng sự của ông đã trình bày vào năm 1935, một tác dụng tức thời như thế trên những cự li xa tùy ý trông có vẻ vi phạm thuyết tương đối, lí thuyết cho rằng không có cái gì có thể truyền đi nhanh hơn ánh sáng. Họ cho rằng nghịch lí này là bằng chứng rằng thuyết lượng tử là chưa hoàn chỉnh.

Nhưng những nhà tiên phong khác phản pháo ngay. Theo Erwin Schrödinger, người đã đặt ra thuật ngữ “vướng víu”, đặc điểm này là nét tiêu biểu thiết yếu của cơ học lượng tử, “đặc điêm khiến nó đi lệch hoàn toàn khỏi hướng tư duy cổ điển”. Phân tích sau đó đã giải được nghịch lí, bằng cách chỉ ra ra rằng các phép đo của một hệ vướng víu thật ra không thể dùng để truyền thông tin nhanh hơn ánh sáng. Và các thí nghiệm trên photon vào những năm 1980 cho thấy sự vướng víu thật sự hoạt động theo kiểu như vậy.

Tuy nhiên, đây thật sự là một phương thức lạ cho Vũ trụ vận hành. Và đây là cái thúc đẩy Fuchs kêu gọi có một cách tiếp cận tươi mới với những nền tảng lượng tử⁴. Ông bác bỏ quan điểm của nhiều nhà nghiên cứu trong lĩnh vực trên rằng các hàm sóng, sự vướng víu và tất cả phần còn lại là biểu diễn cho cái gì đó có thật trong thế giới tự nhiên (xem Nature 485, 157–158; 2012). Thay vậy, mở rộng hướng lập luận đã có từ trường phái Copenhagen, ông khẳng định rằng những cấu trúc toán học này chỉ là một cách định lượng “thông tin cá nhân, kì vọng, mức tin tưởng của nhà quan sát” mà thôi.⁵

Ông được khích lệ theo quan điểm này bởi công trình của Robert Spekkens, một đồng nghiệp của ông tại Viện Perimeter, người đã tiến hành một thí nghiệm tưởng tượng nêu vấn đề vật lí sẽ trông như thế nào nếu vì lí do gì đó tự nhiên hạn chế cái mà bất kì nhà quan sát nào đó có thể biết về một hệ với việc nêu ra “nguyên lí cân bằng kiến thức”: không có thông tin nào của nhà quan sát về hệ, khi đo theo bit, có thể vượt quá lượng thông tin mà người đó thiếu. Các tính toán của Spekkens cho thấy nguyên lí này, trông tùy tiện như nó vốn thế, đủ để tái dựng nhiều đặc điểm của thuyết lượng tử, bao gồm cả sự vướng víu⁶. Những loại ràng buộc khác đối với cái có thể được biết về một bộ trạng thái cũng được chứng minh là tái dựng được các hành trạng giống-lượng tử^7-8.

Khoảng trống kiến thức

Bài học rút ra, theo Fuchs, không phải là mô hình của Spekkens là thực tế - nó chưa bao giờ có nghĩa như thế cả - mà là sự vướng víu và tất cả những hiện tượng lạ lùng khác của thuyết lượng tử không phải là một dạng thức hoàn toàn mới của vật lí học. Chúng có thể phát sinh đơn giản từ một lí thuyết của sự hiểu biết và những hạn chế của nó.

Để hình dung vấn đề rõ ràng hơn, Fuchs đã viết lại thuyết lượng tử bình thường thành một dạng thức tương quan gần gũi với một ngành lí thuyết xác suất cổ điển gọi là suy luận Bayes có xuất xứ vào thế kỉ 18. Theo quan điểm Bayes, xác suất không phải là đại lượng nội tại “gắn liền” với vật. Thay vậy, chúng định lượng mức độ tin tưởng của cá nhân người quan sát về cái có thể xảy ra đối với vật. Quan điểm lượng tử Bayes của Fuchs, viết tắt là QBism^9,10 là một khuôn khổ cho phép những hiện tượng lượng tử đã biết được hồi phục từ những tiên đề mới mẻ không đòi hỏi những cấu trúc toán học ví dụ như hàm sóng. QBism đang thúc đẩy các đề xuất thực nghiệm, ông nói. Những thí nghiệm như thế có thể làm sáng tỏ, chẳng hạn, những cấu trúc mới, sâu sắc bên trong cơ học lượng tử sẽ cho phép các định luật xác suất lượng tử được biểu diễn lại dưới dạng những biến thiên thứ yếu của lí thuyết xác suất chuẩn¹¹.

“Quan điểm mới đó, nếu nó đúng, có thể làm thay đổi sự hiểu biết của chúng ta về cách chế tạo máy tính lượng tử và các bộ công cụ thông tin lượng tử khác,” ông nói. Ông lưu ý rằng những ứng dụng như thế phụ thuộc nhiều vào hành trạng của xác suất lượng tử.

Sự hiểu biết – nó thường được đo theo lượng thông tin mà một nhà quan sát có về một hệ - cũng là tiêu điểm của nhiều cách tiếp cận khác để xây dựng lại thuyết lượng tử. Như các nhà vật lí Časlav Brukner và Anton Zeilinger thuộc trường Đại học Vienna đã chỉ rõ, “vật lí lượng tử là một lí thuyết sơ cấp của thông tin”¹². Trong khi đó, nhà vật lí Marcin Pawłowski tại trường Đại học Gdańsk ở Ba Lan và các đồng sự của ông thì đang khảo sát một nguyên lí họ gọi là “nhân quả thông tin”¹³. Nguyên lí phát biểu rằng nếu một nhà thực nghiệm (gọi là Alice) gửi đi m bit thông tin về dữ liệu của cô ta đến một nhà quan sát khác (Bob), thì Bob có thể thu được không nhiều hơn m bit thông tin cổ điển về dữ liệu đó – cho dù anh ta có thể biết bao nhiêu về thí nghiệm của Alice.

Pawłowski và các đồng sự của ông tìm thấy giả thuyết này được tuân theo bởi vật lí cổ điển và bởi cơ học lượng tử thông thường, nhưng không được tuân theo bởi các lí thuyết thay thế cho phép những dạng mạnh hơn của những tương quan giống-vướng víu giữa các hạt mang thông tin. Vì lí do đó, nhóm của ông viết trong bài báo của họ rằng, “nhân quả thông tin có thể là một trong những tính chất nền tảng của tự nhiên” – nói cách khác, đó là một tiên đề của một lí thuyết lượng tử nào đó được xây dựng lại trong tương lai.

Cái ấn tượng ở một số nỗ lực tái thiết lượng tử này là chúng đề xuất rằng tập hợp các định luật chi phối Vũ trụ của chúng ta chỉ là một trong nhiều khả năng toán học mà thôi. “Hóa ra nhiều nguyên lí dẫn tới cả một họ lí thuyết xác suất, chứ không riêng gì thuyết lượng tử,” Schlosshauer nói. “Rất nhiều đặc điểm chúng ta nghĩ là độc quyền của thuyết lượng tử, nhưng thật ra chúng là tính chất chung cho nhiều lí thuyết xác suất. Điều này cho phép chúng ta tập trung vào câu hỏi cái gì khiến cho thuyết lượng tử là độc nhất vô nhị,” ông nói.

Đã sẵn sàng thành công?

Hardy cho biết tốc độ triển khai của những nỗ lực tái thiết lượng tử đã tăng lên trong vài năm trở lại đây khi các nhà nghiên cứu bắt đầu cảm thấy họ đang có trong tay một số phương tiện tốt để giải quyết vấn đề. “Hiện nay chúng ta đã sẵn sàng cho một số đột phá thật sự quan trọng,” ông nói.

Nhưng liệu ai có thể đánh giá sự thành công của những nỗ lực này? Hardy lưu ý rằng một số nhà nghiên cứu đang tìm kiếm các dấu hiệu thực nghiệm của những tương quan lượng tử bậc cao được phép trong lí thuyết của ông.” Tuy nhiên, tôi muốn nói rằng điều kiện thành công thật sự nghiêng về lí thuyết nhiều hơn,” ông nói. “Liệu chúng ta có hiểu rõ hơn thuyết lượng tử, và liệu các tiên đề có mang đến cho chúng ta những quan điểm mới để vượt ra khỏi nền vật lí ngày nay hay không?” Ông hi vọng rằng một số trong những nguyên lí này cuối cùng có thể hỗ trợ trong sự phát triển của một lí thuyết hấp dẫn lượng tử.

Có rất nhiều chỗ cho người ta hoài nghi. “Việc xây dựng lại thuyết lượng tử từ một tập hợp những nguyên lí cơ bản nghe tựa như một quan điểm với rất nhiều lợi thế,” theo lời nhà vật lí Daniel Greenberger tại trường Cao đẳng Thành phố New York⁵. Nhưng Schlosshauer cho rằng “cho dù không có một chương trình tái thiết đơn lẻ nào thật sự có thể tìm thấy một tập hợp nguyên lí được chấp nhận chung hoạt động được, nhưng đó không phải là một nỗ lực lãng phí, bởi vì chúng ta sẽ học được nhiều điều trên tiến trình cố gắng đó.”

Ông lạc quan nhưng thận trọng. “Một khi chúng ta có một tập hợp những nguyên lí đơn giản và mang tính trực giác vật chất, và một câu chuyện có sức thuyết phục đi cùng với chúng, cơ học lượng tử sẽ trông kém bí ẩn đi nhiều,” ông nói. “Tôi nghĩ rất nhiều câu hỏi nổi bật khi ấy sẽ không còn nữa. Có lẽ tôi không phải là người duy nhất muốn tận mắt chứng kiến người ta khám phá ra những nguyên lí này.”

Trần Nghiêm dịch
Theo Philip Ball (Nature doi:10.1038/501154a)

Tham khảo:

1. Mermin, N. D. Phys. Today 42, 9 (1989).

2. Hardy, L. Bản thảo tại http://arxiv.org/abs/quant-ph/0101012 (2001).

3. Sorkin, R. D. Bản thảo tại http://arxiv.org/abs/gr-qc/9401003 (1994).

4. Fuchs, C. A. Bản thảo tại http://arxiv.org/abs/quant-ph/0106166 (2001).

5. Schlosshauer, M. (ed.) Elegance and Enigma: The Quantum Interviews (Springer, 2011).

6. Spekkens, R. W. Preprint at http://arxiv.org/abs/quant-ph/0401052 (2004).

7. Kirkpatrick, K. A. Found. Phys. Lett. 16, 199–224 (2003).

8. Smolin, J. A. Quantum Inform. Comput. 5, 161–169 (2005).

9. Fuchs, C. A. Bản thảo tại http://arxiv.org/abs/1003.5209 (2010).

10. Fuchs, C. A. Bản thảo tại http://arxiv.org/abs/1207.2141 (2012).