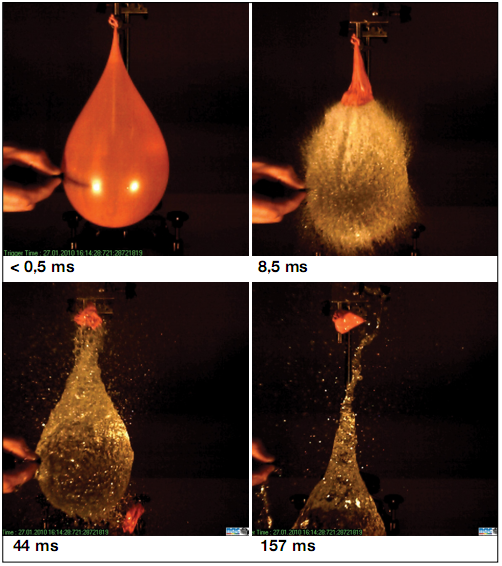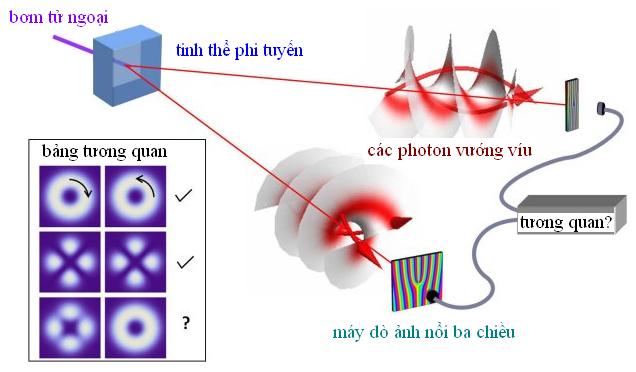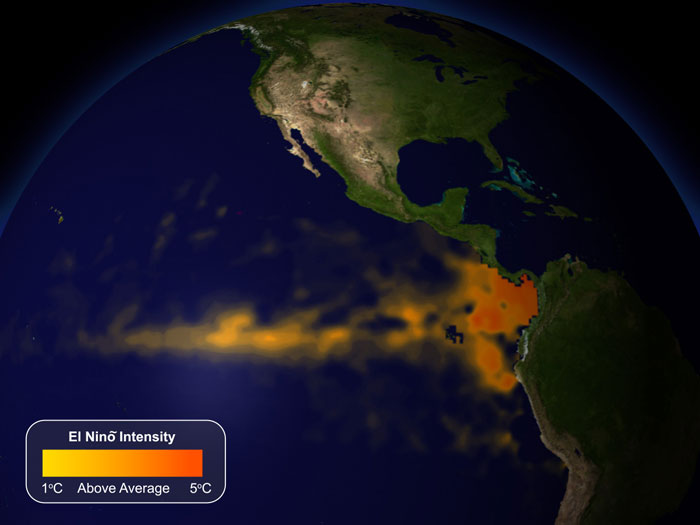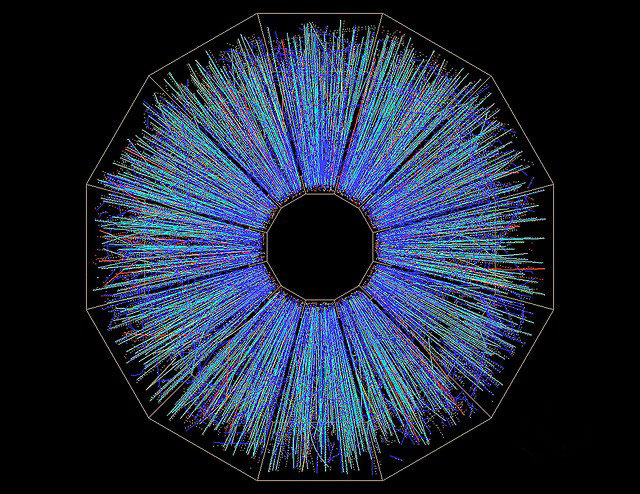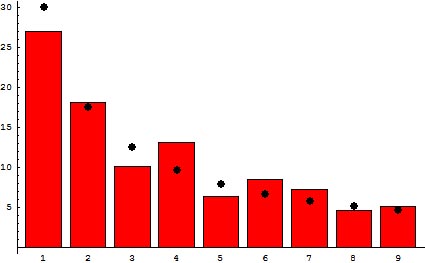
Biểu đồ mô tả tỉ lệ phần trăm các nước có chữ số tương ứng là chữ số đầu tiên của dân số nước đó (các cột màu đỏ). (Ảnh: Jakob Scholbach)
Cái từng được xem đơn giản là một sự hiếu kì toán học có thể trở thành một công cụ khoa học có sức mạnh. Đó là quan điểm của một nhóm nhà địa vật lí, họ nhận thấy rằng định luật Benford – định luật tiên đoán sự phân bố không đều của những chữ số đầu tiên trong các quan sát thế giới thực – thật sự giữ vai trò nào đó trong một nhiều lĩnh vực khác nhau của dữ liệu khoa học. Các nhà nghiên cứu tin rằng việc tìm kiếm các sai lệch khỏi sự phân bố này trong dữ liệu quan sát có thể, thí dụ, làm tăng khả năng xác nhận động đất và cải thiện các mô phỏng máy tính của khí hậu.
Năm 1938, Frank Benford đã khái quát hóa một ý kiến vốn được nêu ra lần đầu bởi nhà thiên văn học thế kỉ thứ 19 Simon Newcomb rằng những chữ số đầu tiên do các quan sát thế giới thực mang lại xuất hiện với xác suất log10(1 + 1/D), trong đó D là giá trị của chữ số đó. Điều này có nghĩa là các con số bắt đầu với số 1 sẽ xuất hiện khoảng 30% thời gian trong tự nhiên, còn tỉ lệ những con số bắt đầu với số 2 sẽ là khoảng 17% và những con số bắt đầu với số 9 chỉ là 4%. Benford cho rằng sự thịnh hành của những chữ số thấp là đúng cho dù viết theo cơ số nào đi nữa, và ông đi tới chứng minh rằng định luật, ngày nay mang tên ông, áp dụng được cho dữ liệu mô tả mọi thứ từ dân cư thành thị cho đến chiều dài của những con sông.
Malcolm Sambridge, một nhà địa chấn học tại trường Đại học quốc gia Australia ở Canberra, phát biểu rằng, nói chung, định luật đó áp dụng được cho dãy số được tạo ra bởi một số loại tiến trình cộng, trong đó những con số lớn ít có khả năng xuất hiện hơn những con số nhỏ. Bỏ qua sự trông đợi theo trực giác của nhiều người rằng sự phân bố của những chữ số đầu tiên là đồng đều, định luật Benford thật ra có ứng dụng thực tiễn là một phương tiện phát hiện gian lận (vì những con số bịa đặt có xu hướng không tuân theo định luật trên). “Khi lần đầu tiên tôi nói với mọi người về điều kiện trên, thường thì phản ứng của họ là đó chắc chắn là một trò lừa đảo”, Sambridge nói. “Nó đơn giản đến mức quái lạ, và thật ra thì nó đúng”.
Từ tia gamma đến sự phát thải khí nhà kính
Trong nghiên cứu mới nhất, Sambridge, làm việc cùng người đồng nghiệp tại trường Đại học quốc gia Australia, Hrvoje Tkalcic và Andrew Jackson ở trường ETH Zürich, nghiên cứu sự phân bố của những chữ số đầu tiên từ 15 bộ dữ liệu chứa tổng cộng hơn 750.000 con số. Những dữ liệu này được trích ra từ nhiều ngành khoa học, đa dạng từ thông lượng photon phát ra từ các nguồn tia gamma xa xôi cho đến sự phát khí thải nhà kính của một nước và số người bị lây nhiễm những căn bệnh khác nhau. Họ nhận thấy mỗi bộ dữ liệu đều tuân theo định luật Benford.
Theo Sambridge, định luật trên có thể dùng để cải thiện các mô phỏng trên máy tính của các quá trình vật lí phức tạp có dữ liệu tuân theo phân bố Benford, thí dụ như dữ liệu cơ sở của khí hậu Trái đất. Các nhà nghiên cứu còn tin rằng định luật trên có giúp phân biệt giữa động đất và các nguồn chấn động khác, thí dụ như các vụ nổ hạt nhân. Họ nhận thấy dữ liệu địa chấn thu từ trận động đất gây ra thảm họa sóng thần châu Á hồi tháng 12 năm 2004, thu thập ở Peru, tuân theo phân bố Benford, còn tín hiệu nhiễu nền có trước trận động đất thì không.
Ngoài ra, bằng cách phân tích dữ liệu do một nhà địa chấn ở Canberra thu thập, họ còn có thể nhận ra một trận động đất nhỏ trước đây không quan sát thấy xảy ra ở thủ đô Australia cùng lúc với trận động đất châu Á. “Hóa ra bạn chẳng phải nghiên cứu các dạng sóng địa chất chi tiết làm gì”, Sambridge nói. “Chỉ những chữ số đầu tiên của dữ liệu dịch chuyển là đủ rồi”.
Có thể áp dụng cho dữ liệu của bạn
Sambridge và các đồng nghiệp thúc giục các nhà khoa học khác nên xem xét kĩ lưỡng dữ liệu của họ nhằm tìm kiếm những kết quả tương tự. Thật vậy, họ nói, định luật Benford “có khả năng phát huy tác dụng trong các khoa học với các tập hợp dữ liệu có ngưỡng động vừa đủ”; nói cách khác là những bộ dữ liệu có giá trị phân tán ít nhất là vài bậc độ lớn, như với trường hợp dữ liệu mà họ đã nghiên cứu.
Tuy nhiên, nhà toán học Theodore Hill thuộc Viện Công nghệ Georgia ở Mĩ vẫn có chút cảnh giác. Ông nói nhóm của Sambridge cung cấp “bằng chứng có sức thuyết phục nữa rằng định luật Benford áp dụng được cho nhiều ngành khoa học”, nhưng ông không tin rằng ngưỡng động đó đủ để xác định xem một bộ dữ liệu có tuân theo định luật đó hay không. Hill đã chứng minh về toán học hồi năm 1995 rằng định luật Benford là định luật vạn vật khả dĩ duy nhất mô tả sự phân bố của các chữ số bất biến dưới những dự biến thiên cấp độ (thí dụ, nó không phụ thuộc chuyện đơn vị trình bày là mét hay kilo mét). Chẳng một ai khác từng phát hiện ra một nguyên lí chung có thể dự đoán chính xác rằng loại tập hợp dữ liệu nào sẽ tuân theo định luật trên. “Tính vạn vật của định luật Benford”, ông nói, “đặc biệt là trong dữ liệu thực, vẫn là bí ẩn”.
Nguồn: physicsworld.com
