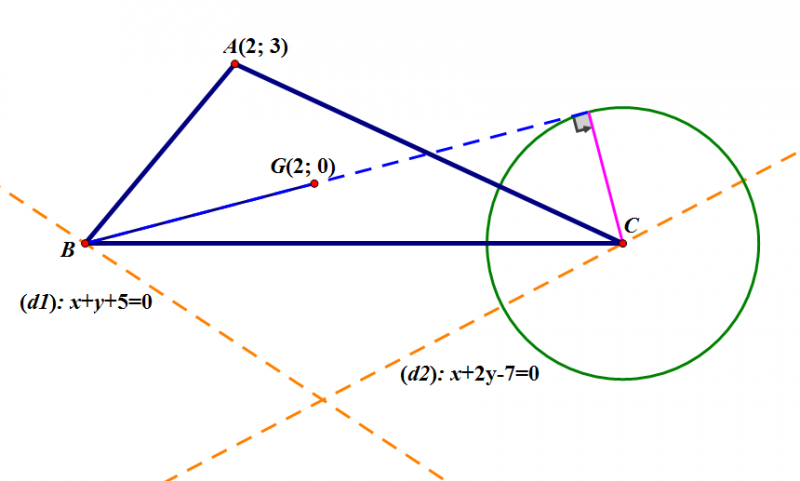
Trong mặt phẳng tọa độ OXY, cho tam giác ABC có điểm A(2;3), trọng tâm G(2;0). Hai đỉnh B và C lần lượt nằm trên hai đường thẳng d1: x+y+5=0 và d2=x+2y-7=0. Viết phương trình đường tròn có tâm C và tiếp xúc với đường thẳng BG.
Mong mn giúp em!
Vì [tex]G[/tex] là trọng tâm [tex]\Delta ABC\Rightarrow \begin{cases}\dfrac{2+b+7-2c}{3}=2\\\dfrac{3-b-5+c}{3}=0\end{cases}\Leftrightarrow \begin{cases}b=-1\\c=1\end{cases}\Rightarrow \begin{cases}B\left(-1;\,-4\right)\\C\left(5;\,1\right)\end{cases}[/tex]
Ta có: [tex]\left(BG\right):\dfrac{x+1}{3}=\dfrac{y+4}{4}\Leftrightarrow 4x-3y-8=0[/tex]
Do đường tròn tâm [tex]C[/tex] tiếp xúc với [tex]\left(BG\right)[/tex] nên khoảng cách từ [tex]C[/tex] đến [tex]\left(BG\right)[/tex] bằng bán kính
[tex]d_{\left(C;\,\left(BG\right)\right)}=\dfrac{\left|4\times 5-3\times 1-8\right|}{\sqrt{4^2+3^2}}=\dfrac{9}{5}[/tex]
Vậy phương trình đường tròn tâm [tex]C[/tex] là: [tex]\boxed{\left(x-5\right)^2+\left(y-1\right)^2=\dfrac{81}{25}}\,.[/tex]
