Cho hình chóp tam giác đều SABC với SA = 2a, AB = a, Gọi H là hình chiếu vuông góc của điểm A trên cạnh SC. Chứng minh SC vuông góc với mặt phẳng (ABH). Tính thể tích khối chóp SABH theo a.
Mọi người giúp mình trả lời với.
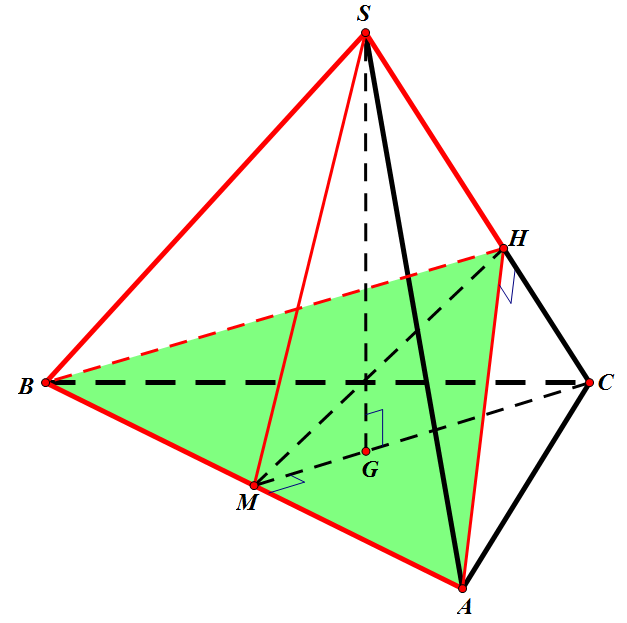
Vì [tex]\Delta ABC[/tex] đều nên [tex]CM\perp AB[/tex] và [tex]G[/tex] là hình chiếu vuông góc của [tex]S[/tex] lên [tex]\left(ABC\right)\Rightarrow SG\perp\left(ABC\right)[/tex]
Ta có: [tex]\left.\begin{matrix}AH\perp SC\\\begin{cases}AB\perp CM\,\,\,\,\,\,\,\,\,\left(\text{cmt}\right)\\AB\perp SG\left(SG\perp\left(ABC\right)\right)\end{cases}\Rightarrow AB\perp\left(SCM\right)\Rightarrow AB\perp SC\end{matrix}\right\}\Rightarrow SC\perp\left(ABH\right)[/tex]
Ta có: [tex]CM=\dfrac{a\sqrt{3}}{2}\Rightarrow CG=\dfrac{a\sqrt{3}}{3}[/tex]
[tex]\Delta SGC[/tex] vuông tại [tex]G\Rightarrow SG=\sqrt{SC^2-GC^2}=\dfrac{a\sqrt{33}}{3}[/tex]
[tex]\Delta SMC[/tex] có: [tex]SG\times MC=MH\times SC\Rightarrow MH=\dfrac{SG\times MC}{SC}=\dfrac{a\sqrt{11}}{4}[/tex]
[tex]\Delta MHC[/tex] vuông tại [tex]H\Rightarrow HC=\sqrt{MC^2-MH^2}=\dfrac{a}{4}\Rightarrow SH=SC-HC=\dfrac{7a}{4}[/tex]
[tex]V_{S.ABH}=\dfrac{1}{3}SH\times S_{AHB}=\dfrac{1}{6}SH\times MH\times AB=\boxed{\dfrac{7a^3\sqrt{11}}{96}}[/tex]
