Câu hỏi về THUYẾT TƯƠNG ĐỐI HẸP

[camthudanvip]

Mọi người cho em hỏi:
Có bài toán anh em sinh đôi chắc hẳn ai cũng biết...
Xin phép nêu lại...
2 anh em sinh đôi, người A ở lại Trái Đất, người B lên tàu vũ trụ bay với vận tốc cận ánh sáng.
Thế cho em hỏi: Khi quay trở về thì ai già ai trẻ.
Vì theo như nêu ra thì B chuyển động với vận tốc cận ánh sáng nên B trẻ hơn.
Nhưng nếu xét hệ quy chiếu gắn với B thì A phải trẻ hơn mới đúng.
Và trên hết: khi search Gu-Gồ thì anh này cho 1 đoạn là: "vào thập niên 1970 người ta đưa một đồng hồ nguyên tử lên quỹ đạo. Khi quay lại Trái đất, nó đã chạy chậm hơn nhiều so với các đồng hồ nguyên tử trên mặt đất"
Kính mong mọi người giúp đỡ để em hiểu thêm về vấn đề này.

[Điền Quang]

Em tham khảo link này:

link

Chúng tôi trích lời bạn Eros ở link trên:

Thực ra việc nói rằng thuyết tương đối hẹp chỉ áp dụng cho các hệ qui chiếu quán tính cho nên ko tính toán được nhiều điều cho cái nghịch lý anh em sinh đôi là một cách giải thích chính xác nhưng lại ... vơ đũa cả nắm. Nó làm mất đi hoàn toàn vẻ đẹp Vật Lý ẩn sau cái nghịch lý nổi tiếng này. Nếu chỉ đơn thuần như vậy thì Langevin đã chẳng mất nhiều công cho nghịch lý này đến thế.

Chúng ta hoàn toàn có thể biết thêm được nhiều điểu về thuyết tương đối hẹp bằng cách mô hình hóa chuyển động của phi hành gia thành 2 pha "đặc biệt" như sau:

-----------------------------------------------------------------------------------------
Hành trình:

Hai anh em sinh đôi (tất nhiên),

E: Người em ở Trái Đất T
A: Người anh phi hành gia khám phá ngôi sao S

Khoảng cách từ S-T là L

- Pha TS: A đi từ T tới S trên một con tàu vũ trụ 1 có vận tốc không đổi là v (không tăng giảm tốc gì cả).

- Pha ST: khi A tới S rồi thì rất nhanh A nhảy lên môt con tàu vũ trụ 2 khác có vận tốc không đổi là -v để trở về T


T------------------------------------------------------------------S
------> lúc đi: vận tốc v trên tàu 1
<------ lúc về: vận tốc -v trên tàu 2

Câu hỏi:

1. Đối với E thì hành trình của pha TS mất bao nhiêu thời gian ? pha ST mất bao nhiêu thời gian ? Thời gian của cả hành trình TST là bao lâu ?

2. Đối với người lái tàu 1 thì hành trình của pha TS mất bao nhiêu thời gian ?

3. Đối với người lái tàu 2 thì hành trình của pha ST mất bao nhiêu thời gian ?

4. Đối với A thì thời gian của hành trình TST là bao lâu ?

Kết luận ai già hơn ai khi gặp nhau ?


5. Nghiệm lại kết quả này bằng việc chỉ sử dụng sự nở dài của thời gian ?

-------------------------

[camthudanvip]

Em cám ơn thầy... em sẽ từ từ ngâm cứu coi sao...

[kemdmt]

[TQTQTQTQ]

[Trần Đức Huy]

Ta chỉ xét đối với các hệ quy chiếu quán tính:
Trước tiên công thức về độ trễ khoảng thời gian giữa hai sự kiện là: [tex]\Delta t=\frac{\Delta t_{0}}{\sqrt{1-\beta ^2}}[/tex]
Trong đó [tex]\Delta t_{0}[/tex] là khoảng thời gian riêng, được định nghĩa là khoảng thời gian giữa hai sự kiện trong HQC [tex]S_{0}[/tex] sao cho hai sự kiện xảy ra tại cùng một điểm trong không gian. Còn [tex]\Delta t[/tex] là khoảng thời gian giữa hai sự kiện trong HQC S chuyển động với vận tốc v đối với HQC [tex]S_{0}[/tex], điều này có thể suy ra dễ dàng bằng cách sử dụng bất biến khoảng: [tex](\Delta s)^2=c(\Delta t)^2-(\Delta x)^2[/tex].
Trở lại với bài giảng số 1. Trong HQC S', hai sự kiện "tia sáng phát ra từ S'" và "tia sáng trở về S'" xảy ra tại cùng một điểm có tọa độ x'=0. Bởi vậy khoảng thời gian giữa hai sự kiện này trong HQC S' cũng chính là khoảng thời gian riêng giữa hai sự kiện này. Bởi vậy ta có công thức: [tex]\Delta t=\frac{\Delta t'}{\sqrt{1-\beta ^2}}[/tex]. Còn hai sự kiện "tia sáng phát ra từ S'" và "tia sáng đập vào gương" trong HQC S' lại diễn ra ở hai điểm có tọa độ khác nhau là x'=0 và x'=L' bởi vậy khoảng thời gian [tex]\Delta t_{1}'[/tex] giữa hai sự kiện này trong HQC S' không phải là khoảng thời gian riêng giữa hai sự kiện này. Bởi vậy ta không có công thức: [tex]\Delta t_{1}=\frac{\Delta t_{1}'}{\sqrt{1-\beta ^2}}[/tex]. Tương tự, ta cũng không có công thức: [tex]\Delta t_{2}=\frac{\Delta t_{2}'}{\sqrt{1-\beta ^2}}[/tex]. Trong trường hợp của hai sự kiện "tia sáng phát ra từ S'" và "tia sáng đập vào gương", bất biến khoảng [tex](\Delta s)^2=0[/tex] nên không tồn tại một HQC nào mà đối với nó hai sự kiện này xảy ra tại cùng một thời điểm hoặc cùng một tọa độ, bởi vì HQC sẽ phải chuyển động với vận tốc ánh sáng. Khoảng cách không gian và khoảng cách thời gian giữa hai sự kiện luôn thỏa mãn hệ thức [tex](\Delta x)^2=c^2(\Delta t)^2[/tex] trong mọi HQC.
Về việc độ trễ của thời gian thì hiệu ứng này đã được kiểm chứng bằng một số thí nghiệm (mà thực nghiệm thì luôn đúng), bạn có thể đọc sơ qua ở đây: http://www.alternativephysics.org/book/TimeDilationExperiments.htm

[mrbap_97]

Có nhiều cách chứng minh công thức của thuyết tương đối. Cách của a post lên là một trong số đó. Gọi là các thí nghiệm tưởng tượng của Enstein. Tuy nhiên cách này theo e rất dễ làm cho người đọc hiểu lầm. Khó phản ánh hết các ngóc ngách của thuyết tương đối hẹp. Ví dụ như khoảng thời gian riêng hay chiều dài riêng, đặc biệt là sự liên hệ giữa tọa độ với thời gian. E nghĩ a nên tìm một số cách chứng minh khác. Cách khiến e thấy dễ hiểu nhất là dẫn từ 2 tiên đề của Enstein, rồi sau đó mới đưa ra các hiện tượng tưởng tượng của Enstein như bài của a post. Chứ không phải đi theo con đường ngược lại.
Tài liệu e nghĩ a nên kham khảo là Vật lý đại cương - Các nguyên lý và ứng dụng tập 3 của thầy Phạm Văn Thiều.

[TQTQTQTQ]

Ta chỉ xét đối với các hệ quy chiếu quán tính:
Trước tiên công thức về độ trễ khoảng thời gian giữa hai sự kiện là: \Delta t=\frac{\Delta t_{0}}{\sqrt{1-\beta ^2}}
Trong đó \Delta t_{0} là khoảng thời gian riêng, được định nghĩa là khoảng thời gian giữa hai sự kiện trong HQC S_{0} sao cho hai sự kiện xảy ra tại cùng một điểm trong không gian. Còn \Delta t là khoảng thời gian giữa hai sự kiện trong HQC S chuyển động với vận tốc v đối với HQC S_{0}, điều này có thể suy ra dễ dàng bằng cách sử dụng bất biến khoảng: (\Delta s)^2=c(\Delta t)^2-(\Delta x)^2.
Trở lại với bài giảng số 1. Trong HQC S', hai sự kiện "tia sáng phát ra từ S'" và "tia sáng trở về S'" xảy ra tại cùng một điểm có tọa độ x'=0. Bởi vậy khoảng thời gian giữa hai sự kiện này trong HQC S' cũng chính là khoảng thời gian riêng giữa hai sự kiện này. Bởi vậy ta có công thức: \Delta t=\frac{\Delta t'}{\sqrt{1-\beta ^2}}. Còn hai sự kiện "tia sáng phát ra từ S'" và "tia sáng đập vào gương" trong HQC S' lại diễn ra ở hai điểm có tọa độ khác nhau là x'=0 và x'=L' bởi vậy khoảng thời gian \Delta t_{1}' giữa hai sự kiện này trong HQC S' không phải là khoảng thời gian riêng giữa hai sự kiện này. Bởi vậy ta không có công thức: \Delta t_{1}=\frac{\Delta t_{1}'}{\sqrt{1-\beta ^2}}. Tương tự, ta cũng không có công thức: \Delta t_{2}=\frac{\Delta t_{2}'}{\sqrt{1-\beta ^2}}. Trong trường hợp của hai sự kiện "tia sáng phát ra từ S'" và "tia sáng đập vào gương", bất biến khoảng (\Delta s)^2=0 nên không tồn tại một HQC nào mà đối với nó hai sự kiện này xảy ra tại cùng một thời điểm hoặc cùng một tọa độ, bởi vì HQC sẽ phải chuyển động với vận tốc ánh sáng. Khoảng cách không gian và khoảng cách thời gian giữa hai sự kiện luôn thỏa mãn hệ thức (\Delta x)^2=c^2(\Delta t)^2 trong mọi HQC.
Về việc độ trễ của thời gian thì hiệu ứng này đã được kiểm chứng bằng một số thí nghiệm (mà thực nghiệm thì luôn đúng), bạn có thể đọc sơ qua ở đây: http://www.alternativephysics.org/book/TimeDilationExperiments.htm

     Đồng ý với Huy. Học sinh lớp 11 mà kiến thức thế này là rất khá.
     Vậy, tôi xin nêu một thắc mắc nữa:
     Theo thuyết tương đối, một hệ qui chiếu quán tính chuyển động dẽ làm không gian của nó co lại theo phương chuyển động.
     Xét 2 điểm A, B đứng yên trên trục x' trong hệ qui chiếu S' chuyển động so với hệ qui chiếu S với vận tốc u tăng dần từ 0.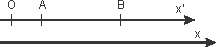
     
     Chúng ta định nghĩa thế nào về vận tốc chuyển động của hệ qui chiếu S' so với hệ qui chiếu S ?
          Giả sử ta định nghĩa rằng, hệ qui chiếu S' chuyển động với vận tốc u so với hệ qui chiếu S khi mọi điểm đứng yên trong S' đều chuyển động với vận tốc u trong hệ qui chiếu S. Trong trường hợp này đối với hệ qui chiếu S ta có; V_A = V_B => V_AB = 0 => AB = const => không gian không bị co lại theo phương chuyển động của hệ qui chiếu.
          Trong trường hợp ta định nghĩa rằng, hệ qui chiếu S' chuyển động với vận tốc u so với hệ qui chiếu S khi gốc tọa độ O của nó chuyển động với vận tốc u trong hệ qui chiếu S. Khi đó, nếu không gian bị co lại theo phương chuyển động thì mọi điểm nằm phía trước của O trên trục Ox' sẽ chuển động với vận tốc nhỏ hơn u trong hệ qui chiếu S, và ngược lại, những điểm nằm sau O (theo phương chuyển động) phải chuyển động với vận tốc lớn hơn u. Như vậy, nếu O nằm giũa AB thì  V_A > u, V_B < u. Nếu O nằm sau AB thì vận tốc của A, B đều nhỏ hơn u vả  V_A > V_B , nếu O nằm trước AB thì vận tốc A,B đều lớn hơn u và V_A < V_B.
Như vậy, vận tốc của A, B tùy thuộc vào vị trí của gốc tọa độ O. Mặt khác, gốc tọa độ trong hệ qui chiếu quán tính là tùy ý chọn. Như vậy, vận tốc của A, B không thể xác định.
     Vậy, có mâu thuẫn gì ở đây, mong các bạn cho ý kiến.
     TQTQTQTQ

[mrbap_97]

Bỏ qua giai đoạn tăng dần từ 0 đến vận tốc u của hệ quy chiếu S' (do hệ quy chiếu S' có gia tốc với hệ quy chiếu S, việc này đc đề cập trong tương đối rộng), chỉ xét giai đoạn chuyển động thẳng đều với vận tốc u. Đồng ý là đoạn AB= const, nhưng tùy vào việc anh đứng trong hệ quy chiếu nào để quan sát chiều dài của thanh AB.

Đứng trong hệ quy chiếu S, tọa độ của các điểm A và B liên hệ với thời gian và tọa độ trong S' theo phép biến đổi Lorentz:
[tex]x'_A= \gamma(x_A+ut_1)[/tex]
[tex]x'_B=\gamma)(x_B+ut_2)[/tex]
Chiều dài của đoạn AB trong hệ nào thì nó phải được đo ở cùng một thời điểm trong hệ quy chiếu đó, do đó: [tex]t_1=t_2[/tex]
[tex]l_0=\gamma l[/tex] hay[tex] l=\frac{l_0}{\gamma[/tex]

Người đứng trong hệ quy chiếu S sẽ luôn thấy thanh có chiều dài l, còn người đứng trong hệ quy chiếu S' sẽ luôn thấy thanh có chiều dài [tex]l_0[/tex]

[mrbap_97]

"Khi đó, nếu không gian bị co lại theo phương chuyển động thì mọi điểm nằm phía trước của O trên trục Ox' sẽ chuển động với vận tốc nhỏ hơn u trong hệ qui chiếu S, và ngược lại, những điểm nằm sau O (theo phương chuyển động) phải chuyển động với vận tốc lớn hơn u."

Câu này e thấy không đúng:  Em hiểu ý anh là trong lúc S' chuyển động so với S thì thấy nó co lại, do đó có sự khác biệt vận tốc. Nhưng trong thuyết tương đối hẹp,  vận tốc của S' so với S phải là hằng số, tức là lúc ta quan sát hiện tượng, S' đã chuyển động vận tốc u không đổi so với S rồi (nói mường tượng là quá trình co lại đã kết thúc). Làm sao anh thấy được quá trình chiều dài nó co lại mà xét đc vận tốc của hai điểm A và B?
Đứng trong S đã mặc định là đo đc l, đứng trong S' đã đo đc [tex]l_0[/tex]. Sau đó hai người đó nói cho nhau nghe thì mới biết nó khác nhau thôi.

[mrbap_97]

 Khoảng cách không gian và khoảng cách thời gian giữa hai sự kiện luôn thỏa mãn hệ thức [tex](\Delta x)^2=c^2(\Delta t)^2[/tex] trong mọi HQC.

Sửa lại tí, bất biến khoảng trong tương đối hẹp
[tex](\Delta s)^2-c^2(\Delta t)^2=(\Delta s')^2-c^2(\Delta t')^2[/tex]

[TQTQTQTQ]

Bỏ qua giai đoạn tăng dần từ 0 đến vận tốc u của hệ quy chiếu S' (do hệ quy chiếu S' có gia tốc với hệ quy chiếu S, việc này đc đề cập trong tương đối rộng), chỉ xét giai đoạn chuyển động thẳng đều với vận tốc u. Đồng ý là đoạn AB= const, nhưng tùy vào việc anh đứng trong hệ quy chiếu nào để quan sát chiều dài của thanh AB.

Đứng trong hệ quy chiếu S, tọa độ của các điểm A và B liên hệ với thời gian và tọa độ trong S' theo phép biến đổi Lorentz:
x'_A= \gamma(x_A+ut_1)
x'_B=\gamma)(x_B+ut_2)
Chiều dài của đoạn AB trong hệ nào thì nó phải được đo ở cùng một thời điểm trong hệ quy chiếu đó, do đó: t_1=t_2
l_0=\gamma l hay l=\frac{l_0}{\gamma

"Khi đó, nếu không gian bị co lại theo phương chuyển động thì mọi điểm nằm phía trước của O trên trục Ox' sẽ chuển động với vận tốc nhỏ hơn u trong hệ qui chiếu S, và ngược lại, những điểm nằm sau O (theo phương chuyển động) phải chuyển động với vận tốc lớn hơn u."

Câu này e thấy không đúng:  Em hiểu ý anh là trong lúc S' chuyển động so với S thì thấy nó co lại, do đó có sự khác biệt vận tốc. Nhưng trong thuyết tương đối hẹp,  vận tốc của S' so với S phải là hằng số, tức là lúc ta quan sát hiện tượng, S' đã chuyển động vận tốc u không đổi so với S rồi (nói mường tượng là quá trình co lại đã kết thúc). Làm sao anh thấy được quá trình chiều dài nó co lại mà xét đc vận tốc của hai điểm A và B?
Đứng trong S đã mặc định là đo đc l, đứng trong S' đã đo đc l_0. Sau đó hai người đó nói cho nhau nghe thì mới biết nó khác nhau thôi.

     Đành rằng thuyết tương đối hẹp chỉ phát biểu cho hệ qui chiếu quán tính, vận tốc u = const, là không gian bị co lại theo phương chuyển động. Nhưng khi hệ qui chiếu S’ bắt đầu chuyển động từ vận tốc u = 0 thì không gian đã bắt đầu phải co lại rồi, chứ không phải đợi cho đến khi u = const mới đột ngột co lại. Bạn có đồng ý với tôi ở điểm này không?
     Cái tôi hỏi ở đây là trong thời kỳ vận tốc u tăng từ 0 tới u = const, chứ không phải là khi u đã ổn định. Tất nhiên bạn có thể nói thuyết tương đối hẹp không xét trường hợp này. Nhưng rõ ràng, đó là hệ quả của nó: khi hệ qui chiếu bắt đầu chuyển động thì không gian đã bắt đầu phải co lại theo phương chuyển động rồi. Nếu vậy thì vấp phải vấn đề mà tôi vừa hỏi.

     Thân ái!
     TQ

[mrbap_97]

    Cái tôi hỏi ở đây là trong thời kỳ vận tốc u tăng từ 0 tới u = const, chứ không phải là khi u đã ổn định. Tất nhiên bạn có thể nói thuyết tương đối hẹp không xét trường hợp này. Nhưng rõ ràng, đó là hệ quả của nó: khi hệ qui chiếu bắt đầu chuyển động thì không gian đã bắt đầu phải co lại theo phương chuyển động rồi. Nếu vậy thì vấp phải vấn đề mà tôi vừa hỏi.

     Thân ái!
     TQ

Em không hề nói nó đột ngột co lại, nhưng e đã nói là lúc S' chuyển động với vận tốc u không đổi với S rồi thì quá trình co lại kết thúc, tức là nó không co nữa, người đứng trong S sẽ luôn thấy nó có chiều dài bao nhiêu đó nhỏ hơn chiều dài riêng. Do đó vận tốc của các điểm A và B hoàn toàn xác định đc.
Cái thứ 2, mọi chuyện trong tương đối hẹp phải bắt đầu từ 2 tiên đề, anh muốn phát biểu điều gì đó cũng phải bắt đầu từ 2 tiên đề. Cũng giống như hình học Ơ- clit, đều phải xuất phát từ các tiên đề rồi mới chứng minh hệ quả của nó. Thuyết tương đối hẹp đã không đụng chạm đến chuyển động có gia tốc của hai hệ quy chiếu rồi, thì anh không thể mang nó mà xét vô được. Và cảm nhận của anh là cảm nhận trực quan, hoàn toàn không có một biểu thức toán học nào chứng minh điều này cả (vì bản thân tiên đề đã không có rồi).
Còn chuyển động có gia tốc của hệ quy chiếu này đối với hệ kia sẽ đc đề cập trong tương đối rộng. Đương nhiên nó sẽ có các tiên đề mới của nó, cũng như một số công cụ toán học cực mạnh như hình học vi phân và tenxo,...Về lý thuyết này e chưa nghiên cứu nên ko trả lời anh được.

[TQTQTQTQ]

Em không hề nói nó đột ngột co lại, nhưng e đã nói là lúc S' chuyển động với vận tốc u không đổi với S rồi thì quá trình co lại kết thúc, tức là nó không co nữa, người đứng trong S sẽ luôn thấy nó có chiều dài bao nhiêu đó nhỏ hơn chiều dài riêng. Do đó vận tốc của các điểm A và B hoàn toàn xác định đc.
Cái thứ 2, mọi chuyện trong tương đối hẹp phải bắt đầu từ 2 tiên đề, anh muốn phát biểu điều gì đó cũng phải bắt đầu từ 2 tiên đề. Cũng giống như hình học Ơ- clit, đều phải xuất phát từ các tiên đề rồi mới chứng minh hệ quả của nó. Thuyết tương đối hẹp đã không đụng chạm đến chuyển động có gia tốc của hai hệ quy chiếu rồi, thì anh không thể mang nó mà xét vô được. Và cảm nhận của anh là cảm nhận trực quan, hoàn toàn không có một biểu thức toán học nào chứng minh điều này cả (vì bản thân tiên đề đã không có rồi).
Còn chuyển động có gia tốc của hệ quy chiếu này đối với hệ kia sẽ đc đề cập trong tương đối rộng. Đương nhiên nó sẽ có các tiên đề mới của nó, cũng như một số công cụ toán học cực mạnh như hình học vi phân và tenxo,...Về lý thuyết này e chưa nghiên cứu nên ko trả lời anh được.

     Tôi không thắc mắc về tiên đề của Einstein ở đây. Một lý thuyết dù tiên đề có đúng nhưng nếu phát triển không tốt vẫn có thể dẫn đến các kết luận sai như thường. Cũng giống như dù công nhận các tiên đề của Ơ-clit cũng vẫn có những kết luận sai nếu học toán dở.
     Ở đây tôi chỉ muốn nói rằng, kết luận về sự co lại của không gian theo phương chuyển động của hệ qui chiếu quán tính trong thuyết tương đối sẽ dẫn đến hệ quả là không gian bị co lại ngay từ khi hệ qui chiếu bắt đầu chuyển động từ vận tốc u = 0 cho tới khi kết thúc ở u = const. Trong khoãng thời gian này sẽ vấp phải vấn đề như tôi đã hỏi.
     Giả sử rằng vấn đề này được giải quyết một cách thỏa đáng thì càng khẳng định tính đúng đắn của thuyết tương đối.
     Trường hợp ngược lại, không giải quyết được vấn đề này, người ta có quyền nghi ngờ tính đúng đắn của thuyết tương đối. Có 2 loại nghi ngờ:
          - Một là nghi ngờ hai tiên đề.
          - Hai là: Không nghi ngờ tiên đề nhưng nghi ngờ quá trình khai triển các tiên đề đó, dẫn đến kết quả sai.
     Đó là những suy nghĩ hoàn toàn khoa học và logic.
     Do đó, tôi đặt vấn đề mong anh chị em trên diễn đàn lý giải giùm chứ chưa dám kết luận vội.
     Thân ái!
     TQ

[ttuethao]

Ta chỉ xét đối với các hệ quy chiếu quán tính:
Trước tiên công thức về độ trễ khoảng thời gian giữa hai sự kiện là: \Delta t=\frac{\Delta t_{0}}{\sqrt{1-\beta ^2}}
Trong đó \Delta t_{0} là khoảng thời gian riêng, được định nghĩa là khoảng thời gian giữa hai sự kiện trong HQC S_{0} sao cho hai sự kiện xảy ra tại cùng một điểm trong không gian. Còn \Delta t là khoảng thời gian giữa hai sự kiện trong HQC S chuyển động với vận tốc v đối với HQC S_{0}, điều này có thể suy ra dễ dàng bằng cách sử dụng bất biến khoảng: (\Delta s)^2=c(\Delta t)^2-(\Delta x)^2.
Trở lại với bài giảng số 1. Trong HQC S', hai sự kiện "tia sáng phát ra từ S'" và "tia sáng trở về S'" xảy ra tại cùng một điểm có tọa độ x'=0. Bởi vậy khoảng thời gian giữa hai sự kiện này trong HQC S' cũng chính là khoảng thời gian riêng giữa hai sự kiện này. Bởi vậy ta có công thức: \Delta t=\frac{\Delta t'}{\sqrt{1-\beta ^2}}. Còn hai sự kiện "tia sáng phát ra từ S'" và "tia sáng đập vào gương" trong HQC S' lại diễn ra ở hai điểm có tọa độ khác nhau là x'=0 và x'=L' bởi vậy khoảng thời gian \Delta t_{1}' giữa hai sự kiện này trong HQC S' không phải là khoảng thời gian riêng giữa hai sự kiện này. Bởi vậy ta không có công thức: \Delta t_{1}=\frac{\Delta t_{1}'}{\sqrt{1-\beta ^2}}. Tương tự, ta cũng không có công thức: \Delta t_{2}=\frac{\Delta t_{2}'}{\sqrt{1-\beta ^2}}. Trong trường hợp của hai sự kiện "tia sáng phát ra từ S'" và "tia sáng đập vào gương", bất biến khoảng (\Delta s)^2=0 nên không tồn tại một HQC nào mà đối với nó hai sự kiện này xảy ra tại cùng một thời điểm hoặc cùng một tọa độ, bởi vì HQC sẽ phải chuyển động với vận tốc ánh sáng. Khoảng cách không gian và khoảng cách thời gian giữa hai sự kiện luôn thỏa mãn hệ thức (\Delta x)^2=c^2(\Delta t)^2 trong mọi HQC.
Về việc độ trễ của thời gian thì hiệu ứng này đã được kiểm chứng bằng một số thí nghiệm (mà thực nghiệm thì luôn đúng), bạn có thể đọc sơ qua ở đây: http://www.alternativephysics.org/book/TimeDilationExperiments.htm

     Đồng ý với Huy. Học sinh lớp 11 mà kiến thức thế này là rất khá.
     Vậy, tôi xin nêu một thắc mắc nữa:
     Theo thuyết tương đối, một hệ qui chiếu quán tính chuyển động dẽ làm không gian của nó co lại theo phương chuyển động.
     Xét 2 điểm A, B đứng yên trên trục x' trong hệ qui chiếu S' chuyển động so với hệ qui chiếu S với vận tốc u tăng dần từ 0.
     
     Chúng ta định nghĩa thế nào về vận tốc chuyển động của hệ qui chiếu S' so với hệ qui chiếu S ?
          Giả sử ta định nghĩa rằng, hệ qui chiếu S' chuyển động với vận tốc u so với hệ qui chiếu S khi mọi điểm đứng yên trong S' đều chuyển động với vận tốc u trong hệ qui chiếu S. Trong trường hợp này đối với hệ qui chiếu S ta có; V_A = V_B => V_AB = 0 => AB = const => không gian không bị co lại theo phương chuyển động của hệ qui chiếu.
          Trong trường hợp ta định nghĩa rằng, hệ qui chiếu S' chuyển động với vận tốc u so với hệ qui chiếu S khi gốc tọa độ O của nó chuyển động với vận tốc u trong hệ qui chiếu S. Khi đó, nếu không gian bị co lại theo phương chuyển động thì mọi điểm nằm phía trước của O trên trục Ox' sẽ chuển động với vận tốc nhỏ hơn u trong hệ qui chiếu S, và ngược lại, những điểm nằm sau O (theo phương chuyển động) phải chuyển động với vận tốc lớn hơn u. Như vậy, nếu O nằm giũa AB thì  V_A > u, V_B < u. Nếu O nằm sau AB thì vận tốc của A, B đều nhỏ hơn u vả  V_A > V_B , nếu O nằm trước AB thì vận tốc A,B đều lớn hơn u và V_A < V_B.
Như vậy, vận tốc của A, B tùy thuộc vào vị trí của gốc tọa độ O. Mặt khác, gốc tọa độ trong hệ qui chiếu quán tính là tùy ý chọn. Như vậy, vận tốc của A, B không thể xác định.
     Vậy, có mâu thuẫn gì ở đây, mong các bạn cho ý kiến.
     TQTQTQTQ

Trong phép biến đổi liên hệ các hệ quy chiếu quán tính vận tốc u là một tham số của phép biến đổi. Trước hết nó đặc trưng cho phép biến đổi. Sau đó mới đến việc tham số này được lý giải vật lý thế nào. Ở đây u có thể được lý giải như vận tốc của một điểm bất kỳ đứng yên trong S' sẽ chuyển động đối với người quan sát trong S.

Đối với trường hợp bạn nói thì vấn đề khác. Hệ quy chiếu S' không phải là một hệ quy chiếu quán tính, do đó nó không đặc trưng đơn thuần bởi một tham số (u). Việc mỗi điểm đứng yên trong S sẽ được nhìn thấy với vận tốc khác nhau trong S' là hoàn toàn bình thường. 

[ttuethao]

PS: (bổ sung thêm cho rõ) xét phép biến đổi hệ quy chiếu quán tính sang hệ quy chiếu quay trong cơ học cổ điển. Ở đó mỗi một điểm của hệ quy chiếu quay cũng có một vận tốc khác nhau đối với hệ quy chiếu quán tính. Điều này không có gì lạ cả: vận tốc không phải một tham số đặc trưng của phép biến đổi tọa độ này (mà là vận tốc góc). 

[mrbap_97]

     Tôi không thắc mắc về tiên đề của Einstein ở đây. Một lý thuyết dù tiên đề có đúng nhưng nếu phát triển không tốt vẫn có thể dẫn đến các kết luận sai như thường. Cũng giống như dù công nhận các tiên đề của Ơ-clit cũng vẫn có những kết luận sai nếu học toán dở.
     Ở đây tôi chỉ muốn nói rằng, kết luận về sự co lại của không gian theo phương chuyển động của hệ qui chiếu quán tính trong thuyết tương đối sẽ dẫn đến hệ quả là không gian bị co lại ngay từ khi hệ qui chiếu bắt đầu chuyển động từ vận tốc u = 0 cho tới khi kết thúc ở u = const. Trong khoãng thời gian này sẽ vấp phải vấn đề như tôi đã hỏi.
     Giả sử rằng vấn đề này được giải quyết một cách thỏa đáng thì càng khẳng định tính đúng đắn của thuyết tương đối.
     Trường hợp ngược lại, không giải quyết được vấn đề này, người ta có quyền nghi ngờ tính đúng đắn của thuyết tương đối. Có 2 loại nghi ngờ:
          - Một là nghi ngờ hai tiên đề.
          - Hai là: Không nghi ngờ tiên đề nhưng nghi ngờ quá trình khai triển các tiên đề đó, dẫn đến kết quả sai.
     Đó là những suy nghĩ hoàn toàn khoa học và logic.
     Do đó, tôi đặt vấn đề mong anh chị em trên diễn đàn lý giải giùm chứ chưa dám kết luận vội.
     Thân ái!
     TQ

Chính sự thiếu sót là không thể lý giải chuyển động có gia tốc của hệ quy chiếu, nên Enstein mới phát triển lý thuyết tương đối hẹp của mình lên thành tương đối rộng. Căn bản nó là một lý thuyết chưa hoàn chỉnh. Câu hỏi của anh rõ ràng là vô nghĩa, kiểu như: Trong tập hợp 3 số {1;2;3} thì số 4 có phải là số lớn nhất hay không vậy.
Nếu anh muốn nói về chuyển động có gia tốc, thì đúng ra anh nên nói là: Trong thuyết tương đối rộng, sự chuyển động có gia tốc sẽ gây ra hậu quả gì? Và anh nên nghiên cứu về tương đối rộng chứ không phải tương đối hẹp.
Chứ không phải là :"Thuyết tương đối hẹp, sự chuyển động có gia tốc sẽ như thế nào?" - Như vậy là vô nghĩa.
Lý thuyết hoàn thiện nhất vẫn là tương đối rộng, thiết nghĩ nếu anh nghiên cứu hoàn thiện thuyết tương đối rộng rồi thì bắt bẻ Entein cũng chưa muôn  BIết đâu lại có 1 giải Noben

[TQTQTQTQ]

          Chúng ta hãy bình tĩnh xét vấn đề cho thật khách quan.
     Tuy thuyết tương đối hẹp chỉ xét cho hệ qui chiếu quán tính, nhưng hệ quả của nó là: không gian bị co lại khi hệ qui chiếu chuyển động với gia tốc dương. Cái hệ quả này vấp phải mâu thuẫn và tôi tham khảo ý kiến của anh chị em trên diễn đàn chứ không có ý gì khác
     Do đó, các câu trả lời về biến đổi tọa độ không đi vào nội dung câu hỏi. Còn mrbap_97 nói là vấn đề được giải quyết trong thuyết tương đối rộng thì tôi cũng coi như là một câu trả lời đúng nội dung. Nhưng điều đó có nghĩa là, bản thân thuyết tương đối hẹp không giải quyết được vấn đề của chính nó phát sinh mà phải viện dẫn đến một lý thuyết khác (cho dù cùng một tác giả là Einstein vĩ đại). Trong trường hợp ấy, thông thường giới khoa học sẽ không công nhận lý thuyết đó đúng.
     Tuy nhiên, khi tôi đưa câu hỏi lên diễn đàn là tôi kỳ vọng câu trả lời từ tất cả các thành viên, bao gồm cả những cao nhân giỏi về thuyết tương đối rộng. Tôi cũng muốn lý thuyết này đúng thì nhân loại đỡ nhiều công sức đã học tinh thông nó, chứ nếu sai phải học lại cái khác thì cũng khổ lắm. Nhưng khoa học vốn khách quan, công bằng nên mình thấy mâu thuẫn thì mình cứ hỏ thôi.
     Thân ái!
     TQ

[mrbap_97]

Một lý thuyết được chấp nhận là một lý thuyết giải thích được cho một số hiện tượng, vì hiện giờ làm gì có lý thuyết giải thích hết các hiện tượng xảy ra trong tự nhiên đâu  :.)). Ở bậc vật lý hiện đại, mọi lý thuyết đều có thể bị nghi ngờ vì chưa ai kiểm chứng được nó hoàn toàn đúng đắn. Vì ngay cả quá trình thực hiện thí nghiệm cũng đã mất 10 năm, 20 năm hoặc cả đời một nhà nghiên cứu rồi.
Rõ ràng vật lý cổ điển Niuton là một lý thuyết sai, nhưng nó vẫn được áp dụng trong trường hợp chuyển động có vận tốc nhỏ hơn c rất nhiều. Nên vẫn có chỗ đứng cho đến ngày nay. Và nếu vận tốc nhỏ hơn c thì người ta áp dụng cổ điển vào chứ không ai lại đi áp dụng công thức thuyết tương đối vào cho phức tạp vấn đề.
Cũng như tương đối hẹp, chỉ cần chuyển động ko có gia tốc thì nó vẫn áp dụng được. Và nó là trường hợp đặc biệt của tương đối rộng khi a=0. Không ai tự nhiên lại đi làm khó mình cả. Trong lý thuyết tương tối rộng đã đề cập đến sóng hấp dẫn, và sau khi Enstein mất mấy chục năm rồi mới phát hiện được, một phần đã xác giúp kiểm chứng tính đúng đắn của nó.
Một mô hình sai nhưng vẫn được sử dụng cho đến ngày nay chính là mẫu nguyên tử Borh. Mẫu nguyên tử này đúng cho sự phát xạ các vạch bức xạ của nguyên tử H, nếu nghiên cứu về H thì hoàn toàn có thể áp dụng lý thuyết này vào. Nhưng lại là sự kết hợp "nửa nạc nửa mỡ" giữa vật lý cổ điển và vật lý hiện đại. (Dùng lực điện cổ điển và lượng tử hóa trong vật lý hiện đại) Sau này hoàn thiện hơn mới đưa ra lý thuyết về hàm sóng.
Cũng như dự đoán về tính chất lưỡng tính của vật thể do De Broglie, vì nó quá nhỏ ko thể dùng các dụng cụ để đo được, nhưng vẫn tìm ra được nhờ một thí nghiệm trung gian.
P/s: bài học rút ra của em là khi học Vật lý không nên quá cứng nhắc vào một lý thuyết và cho nó hoàn toàn đúng, xem xét hoàn cảnh rồi mới rút ra trường hợp nào cần dùng, trường hợp nào không nên dùng.  

[ttuethao]

OK, nói nhiều cũng không rõ ràng hơn được. Ca hai bạn có thể tham khảo bài sau vể Bell's spaceship, cũng là một thảo luận thú vị:
 
https://en.wikipedia.org/wiki/Bell%27s_spaceship_paradox#cite_note-fayngold-4

[TQTQTQTQ]

Một lý thuyết được chấp nhận là một lý thuyết giải thích được cho một số hiện tượng, vì hiện giờ làm gì có lý thuyết giải thích hết các hiện tượng xảy ra trong tự nhiên đâu  . Ở bậc vật lý hiện đại, mọi lý thuyết đều có thể bị nghi ngờ vì chưa ai kiểm chứng được nó hoàn toàn đúng đắn. Vì ngay cả quá trình thực hiện thí nghiệm cũng đã mất 10 năm, 20 năm hoặc cả đời một nhà nghiên cứu rồi.
Rõ ràng vật lý cổ điển Niuton là một lý thuyết sai, nhưng nó vẫn được áp dụng trong trường hợp chuyển động có vận tốc nhỏ hơn c rất nhiều. Nên vẫn có chỗ đứng cho đến ngày nay. Và nếu vận tốc nhỏ hơn c thì người ta áp dụng cổ điển vào chứ không ai lại đi áp dụng công thức thuyết tương đối vào cho phức tạp vấn đề.
Cũng như tương đối hẹp, chỉ cần chuyển động ko có gia tốc thì nó vẫn áp dụng được. Và nó là trường hợp đặc biệt của tương đối rộng khi a=0. Không ai tự nhiên lại đi làm khó mình cả. Trong lý thuyết tương tối rộng đã đề cập đến sóng hấp dẫn, và sau khi Enstein mất mấy chục năm rồi mới phát hiện được, một phần đã xác giúp kiểm chứng tính đúng đắn của nó.
Một mô hình sai nhưng vẫn được sử dụng cho đến ngày nay chính là mẫu nguyên tử Borh. Mẫu nguyên tử này đúng cho sự phát xạ các vạch bức xạ của nguyên tử H, nếu nghiên cứu về H thì hoàn toàn có thể áp dụng lý thuyết này vào. Nhưng lại là sự kết hợp "nửa nạc nửa mỡ" giữa vật lý cổ điển và vật lý hiện đại. (Dùng lực điện cổ điển và lượng tử hóa trong vật lý hiện đại) Sau này hoàn thiện hơn mới đưa ra lý thuyết về hàm sóng.
Cũng như dự đoán về tính chất lưỡng tính của vật thể do De Broglie, vì nó quá nhỏ ko thể dùng các dụng cụ để đo được, nhưng vẫn tìm ra được nhờ một thí nghiệm trung gian.
P/s: bài học rút ra của em là khi học Vật lý không nên quá cứng nhắc vào một lý thuyết và cho nó hoàn toàn đúng, xem xét hoàn cảnh rồi mới rút ra trường hợp nào cần dùng, trường hợp nào không nên dùng. 

     Bạn rất tỉnh táo và cầu thị.
     Nói chung, về vấn đề này cũng không có gì khó khăn cả. Theo tôi, kết luận về sự co lại của không gian khi hệ qui chiếu chuyển động là một sai lầm. Cho đến nay, người ta kiểm chứng được sự co lại của thời gian nhưng chưa từng phát hiện sự co lại của không gian trong chuyển động. Thực ra, không gian không hề bị co lại vì chuyển động. Tuy nhiên, thời gian thì co lại theo chuyển động nhưng độ co lại phụ thuộc phương chuyển động chứ không đồng đều cho mọi phương, và dẫn đến không có cái gọi là tính không đồng bộ về thời gian.
      Nói cách khác, không thể có một trục thời gian cho 3 trục không gian mà mỗi một phương không gian có một trục thời gian riêng không giống nhau. Thuyết tương đối hẹp phạm sai lầm này và để bảo đảm tính hợp lý, người ta đưa ra khái niệm không đồng bộ về thời gian và dẫn đến tính tương đối của nhiều khái niệm như  trước, sau, to, nhỏ, lớn, bé,…  rất khó hiểu nhưng lại được cho là trí tuệ cao siêu…
     Bạn nói đúng, để thực nghiệm kiểm chứng thì rất lâu, nhưng ít nhất, về logic trong lý thuyết phải hợp lý, không mâu thuẫn. Nhưng kinh nghiệm cho tôi thấy, khai phá một cái mới đã khó khăn nhưng thuyết phục thiên hạ từ bỏ cái cũ, sai lầm để theo cái mới, đúng đắn còn khó khăn hơn nhiều.
     Ví dụ như ai cũng biết, trong sinh hoạt của mình, chúng ta coi Trái đất là hệ qui chiếu đứng yên. Nhưng trong hệ Mặt trời thì Mặt trời được coi là đứng yên. Trong Thiên hà thì Trung tâm Thiên hà được cọi là hệ qui chiếu đứng yên…. Cứ qui nạp lên mãi, phải chăng chúng ta sẽ tìm được một hệ qui chiếu đứng yên trong toàn Vũ trụ? hay ít nhất, chúng ta có thể giả thiết về sự tồn tại một hệ qui chiếu đứng yên tuyệt đối trong Vũ trụ, sau đó dùng thực nghiệm để chứng minh sự tồn tại đó. Và như thế, chúng ta sẽ có một “thuyết tuyệt đối”. Thực sự, chúng ta đã có thực nghiệm chứng minh điều đó rồi, nhưng với quan niệm thuyết tương đối ăn sâu vào óc, ta lại cho cái bằng chứng thực nghiệm ấy là một nghịch lý!!!  Cái thực nghiệm ấy chính là con lắc Foucault từ thế kỳ 19 (năm 1851). Cho tới tận bây giờ, vẫn chỉ có thuyết tương đối và con lắc Foucault vẫn chỉ là một nghịch lý!
Vài lời chia sẻ.
TQ

[TQTQTQTQ]

     Anh chị em trên  diễn đàn thân mến.
     Như vậy, tôi đã chỉ ra một hệ quả không hợp lý của thuyết tương đối, mấy hôm nay không thấy ai phản hồi gì. Phải chăng đó là sự thật hay do giới hạn kiến thức, hay không ai thèm trả lời. Về lý do cuối thì tôi không tin lắm vì trong các bài viết của mình, tôi luôn chú ý từ nghữ để không đắc tội với ai. Lý do thứ 2 cũng không vững chắc vì không người này thì người khác có đủ kiến thức chứ. Vậy có lẽ là do thực sự đó là mâu thuẫn không giải quyết được của thuyết tương đối, nhưng do danh tiếng và vị thế của Einstein và những người tin theo quá lớn, cộng thêm tâm lý tự ty nên không ai có ý kiến gì chăng? Nhưng tinh thần khoa học là khách quan và công bằng, do đó tôi rất mong anh chị em cho ý kiến.
Thân ái!
TQ

[TQTQTQTQ]

Tôi có một công trình khá lớn về Vật lý lý thuyết, không biết làm cách nào công bố một cách hiệu quả. Kính nhờ anh chị em trên diễn đàn tư vấn.
Cám ơn!
Nội dung công trình:
- Những qui luật tổng quá nhất trong Vũ trụ
- Thuyết tuyệt đối (thay thế thuyết tương đối, nhưng vẩn công nhận vận tốc ánh sáng là c trong mọi HQC quán tính. Tuy nhiên, có giải thích tại sao vận tốc ánh sáng lại là c = const)
- Một phần thuyết lượng tử (nguyên lý bất định, tính sóng hạt, phương trình hàm sóng)
- Sự hình thành và phát triển của Vũ trụ từ khởi nguyên.
Với nhiều phương trình và kết luận động chạm tới nền tảng căn bản nhất của vật lý, có thể ứng dụng cho các tính toán trong điều kiện trường hấp dẫn quá lớn, giải quyết rốt ráo vấn đề năng lượng tối (năng lượng có thể làm cho Vũ trụ nở ra) ...

[nthlqt]

Thuyết tương đối đã đem lại cách xem xét "thế giới" ở dạng bốn chiều theo nghĩa không-thời gian , bởi vì theo lý thuyết này thời gian đã bị cướp mất tính độc lập của nó, như phương trình của phép biến đổi Lỏrentz.

"Khoảng cách không gian" thuần túy của hai hiện tượng(A,B) đối với K(HQC đứng yên) đã sinh ra hệ quả là một "khoảng cách thời gian" của cùng các hiện tượng đối với K’(HQC chuyển động). Thời Toạ độ thời gian trong không- thời gian 4 chiều đóng vai tro như 3 toạ độ ko gian. Vì thế sự giãn nở thời gian cua K'(chứ ko phảo co lại như anh nói) cũng chính là sự co lại của không gian dc nhìn từ K. Vì thế việc anh nói vận tốc ko làm không gian co lại là ko đúng.

[TQTQTQTQ]

          Nói đi nói lại thì Thuyết tương đối, kể cả rộng lẫn hẹp, không thể mô tả được một vấn đề hết sức đơn giản là: thế nào là chuyển động của một hệ qui chiếu K' so với Hệ qui chiếu K với vận tốc u khác const, khi có kết luận không gian bị co lại vì vận tốc u đó, vì sẽ vấp phải mâu thuẫn như tôi đã trình bày ở bài trước. Điều đó chứng tỏ sự sai lầm của Thuyết tương đối.
          Vấn đề là ở chỗ, trong khai triển logic của mình, Thuyết tương đối đã sai lầm ở đâu ?
          Khi nghiên cứu khai triển logic toán học về lý thuyết của Thuyết tương đối, được viết trong giáo trình đại học, tôi đã chỉ ra sai lầm của các nhà khoa học trong bài " Về sai lầm của Thuyết tương đối ngay trong khai triển lý thuyết"  tại địa chỉ http://thuvienvatly.com/forums/index.php?topic=25796.30 ngay trên diễn đàn này. Mời các bạn tham khảo.
          Chính vì vậy, tôi đã đề xuất THUYẾT TUYỆT ĐỐI cũng trên diễn đàn này. Mời các bạn cho ý kiến!
          Thân ái!

[Lê Quý]

- Tôi thực sự tiếc những không gian trao đổi học thuật trên forum như thế này giừo đây bị lấn lướt bởi những Comment hời hợt trên facebook. Khiến cho những lúc cần trao đổi thảo luận mà ko biết trao đổi với ai.
- Quy trở lại chủ đề chính, nghịch lý anh em sinh đôi được chính Einsteins đưa ra như một ví dụ để minh chúng rằng bạn chưa hiểu thuyết tương đối. Bởi vì đa số mọi người học thuyết tương đối khi nhìn vào các biến đổi chứng minh của nó đều dễ dãi nhận định rằng "tôi đã hiểu" , nhưng khi Einstein đưa ra nghịch lý này để mọi người đưa công thức vào tính thì mọi người mới thấy mình chả hiểu gì. Có thể nói, một người hiểu được thuyết tương đối hẹp phải là một người hiểu được nghịch lý anh em sinh đôi.
- đầy người cũng dễ dãi cho rằng mình hiểu nghịch lý anh em sinh đôi nhưng sau khi thảo luận một thôi một hồi họ chợt nhận ra mình không hiểu gì. Vậy thế nào là một người hiểu nghịch lý anh em sinh đôi? Câu trả lời phải là người chỉ được ra đâu là nghịch lý/ và giải thích được tại sao trước đấy ta lại thấy nó là nghịch lý!
- đa số mọi người học xong còn không biết đâu là nghịch lý của twin paradox.
- nói thật là cho đến gần đây tôi cũng ko tin lắm có ai có thể hiểu được nghịch lý này. (Kể cả tác giả của nó) . tôi cũng thắc mắc như chủ thớt và quan điểm của tôi là nếu ta chưa hiểu thì ta cũng cố gắng diễn giải xem mình đang khó hiểu ở chỗ nào. Chúng ta nên cùng nhau thống nhất về những luận điểm những hiện tượng nào trong nghịch lý này.
- ở đây tôi có nói  băn khoăn của mình đây. Mọi người cùng vào thảo luận nhé!
https://youtu.be/DLU647e8R9o