Mới nghĩ ra 1 hướng giải quyết nhưng vẫn còn nhiều băn khoăn chưa chắc chắn, mình xin nêu ra đây mong thầy cô và các bạn góp ý!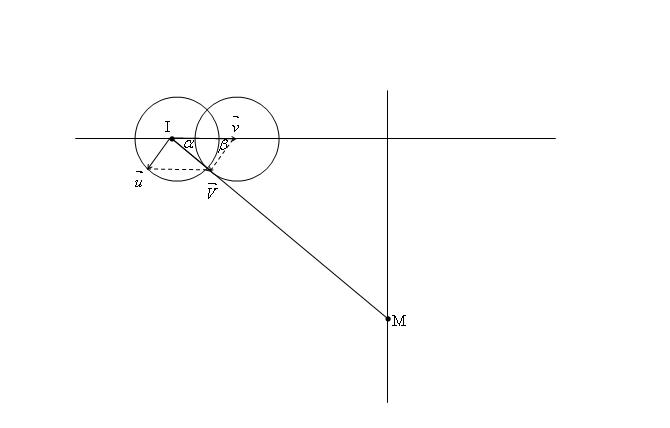
+ Gọi v, u và V là vận tốc của máy bay, âm thanh đối với máy bay và âm thanh đối với đất. Ta có: [tex]V = \frac{usin\beta }{sin\alpha }[/tex]
+ Xét máy bay ở vị trí bất kì. Thời gian truyền âm từ vị trí I đến điểm M: [tex]t=\frac{s}{V}=\frac{\frac{s_1}{sin\alpha }}{\frac{usin\beta }{sin\alpha }}=\frac{s_1}{usin\beta }[/tex] => tmin khi sin[tex]\beta[/tex]max
Mặt khác do u < v nên từ hình vẽ ta thấy sin[tex]\beta[/tex]max khi máy bay ở điểm I tại đó u vuông góc với V. Vì khi máy bay lại gần giao điểm của quỹ đạo với MN thì âm không thể tới M ( đường tròn tâm là điểm mút của V không cắt IM nên V sẽ ko thuôc IM)
==> [tex]t_{1min}= \frac{s_1}{u\frac{\sqrt{v^2-u^2}}{v}}[/tex]
+ Tương tự cho điểm N: [tex]t_{2min}= \frac{s_2}{u\frac{\sqrt{v^2-u^2}}{v}}[/tex]
+ Theo bài ra: [tex]t_{2min} - t_{1min}=t[/tex] và [tex]s_{2} - s_{1}[/tex] = L: [tex]\frac{v}{u\sqrt{v^2-u^2}}L=t[/tex]
==> [tex]v=\frac{u^2t}{\sqrt{(ut)^2-L^2}}[/tex]

