I - VẬN TỐC TỨC THỜI. CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU (CĐTBĐĐ)

 1. Độ lớn của vận tốc tức thời

  Một ôtô con chạy từ Hà Nội đến Hải Phòng trên quãng đường dài s = 105 km trong khoảng thời gian t = 2 giờ 30 phút. Chiếc xe chạy trên đường thẳng có lúc nhanh, có lúc chậm. Đại lượng vật lí nào sẽ cho biết ôtô con chạy nhanh hay chạy chậm?

  Độ lớn vận tốc tức thời v  của một vật chuyển động tại một điểm M là đại lượng đo bằng thương số giữa đoạn đường rất nhỏ Δs đi qua M và khoảng thời gian rất ngắn Δt để vật đi hết đoạn đường đó. Độ lớn vận tốc tức thời tại M cho ta biết sự nhanh chậm của chuyển động tại M.

  Đại lượng: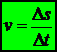

  là độ lớn của vận tốc tức thời (m/s hoặc km/h).

  Δs: quãng đường đi được rất nhỏ (m hoặc km).

  Δv: thời gian rất nhỏ đi hết quãng đường đó (s hoặc h).

  Cũng có thể nói: Độ lớn vận tốc tức thời của xe tại M là vận tốc trung bình cuả xe trên đoạn đường rất ngắn qua M.

  Trên xe máy, đồng hồ tốc độ (còn gọi là tốc kế) luôn luôn chỉ độ vận tốc tức thời của xe (Hình 3.1b).

Hình 3.1a. Tốc kế trên ô tô (giữa)

Hình 3.1b. Tốc kế trên xe máy

  2. Vectơ vận tốc tức thời

 Cùng một lúc, một máy bay bay về hướng bắc với tốc độ 700 km/h, một máy bay bay về hướng tây với tốc độ 500 km/h (Hình 3.2). Như vậy, hai máy bay khác nhau cả về độ lớn vận tốc tức thời và phương, chiều.

  Vectơ vận tốc tức thời là một đại lượng vectơ có:

- Gốc đặt ở vật chuyển động

- Phương và chiều là phương và chiều của chuyển động.

- Độ dài biểu diễn độ lớn của vận tốc theo một tỉ xích nào đó.

* Chú ý: Khi nhiều vật chuyển động trên một đường thẳng theo hai chiều ngược nhau, ta phải chọn một chiều dương trên đường thẳng trên và quy ước như sau:

- Vật chuyển động theo chiều dương có v > 0.

- Vật chuyển động ngược chiều dương có v < 0.

- Tốc độ và vận tốc thường được xem là có cùng một ý nghĩa. Nhưng trong Vật Lí, hai đại lượng này có những điểm khác nhau: Vận tốc là tốc độ của chuyển động trên một hướng xác định.

- Khi nói  vận tốc của vật tại vị trí hoặc thời điểm nào đó, ta hiểu là vận tốc tức thời.
- Khi nói: xe di chuyển 60 km/h đấy là nói tới tốc độ. Trong trường hợp nói: Chiếc xe di chuyển 60 km/h về phía Bắc đây là đang nói đến vận tốc. Vậy, độ lớn của vận tốc còn được gọi là tốc độ chuyển động, nếu muốn nói về cả phương và chiều của vận tốc thì bắt buộc phải dùng thuật ngữ vận tốc.

Hình 3.2

Hình 3.3

 3. Chuyển động thẳng biến đổi đều

 Chuyển động thẳng biến đổi là chuyển động có quỹ đạo là đường thẳng và có độ lớn vận tốc tức thời luôn luôn biến đổi.

  Loại chuyển động thẳng biến đổi đơn giản nhất là chuyển động thẳng biến đổi đều. Trong chuyển động thẳng biến đổi đều thì vận tốc tức thời có độ lớn tăng hoặc giảm đều theo thời gian.

  Chuyển động thẳng có độ lớn vận tốc tăng dần đều theo thời gian gọi là chuyển động thẳng nhanh dần đều (Bảng 3.1).

  Chuyển động thẳng có độ lớn vận tốc giảm dần đều theo thời gian gọi là chuyển động thẳng chậm dần đều (Bảng 3.2).

II - CHUYỂN ĐỘNG THẲNG NHANH DẦN ĐỀU (CĐTNDĐ)

 1. Gia tốc trong chuyển động thẳng nhanh dần đều

  Trong quá trình chuyển động, vận tốc của chất điểm có thể thay đổi cả về độ lớn cũng như về phương và chiều. Chẳng hạn ô tô rời điểm xuất phát và viên đạn chuyển động trong nòng súng đều chuyển động nhanh dần nhưng vận tốc của viên đạn tăng nhanh hơn ô tô hay vật đang chuyển động chậm dần rồi quay lại. Để đặc trưng cho sự thay đổi của vận tốc theo thời gian, người ta đưa thêm vào một đại lượng vật lí mới gọi là gia tốc.

  a) Khái niệm gia tốc

  Để đơn giản ta xét chuyển động thẳng. Gọi v₁ là vận tốc của vật lúc bắt đầu tăng (hoặc giảm). Sau khoảng thời gian Δt rất nhỏ, vận tốc đạt đến giá trị v₂ (Hình 3.4).

  Hiệu Δv = v₂ – v₁ gọi là độ biến thiên của vận tốc.

  Đại lượng:

    (3.1a)

gọi là gia tốc của chuyển động. Nó cho biết sự biến thiên nhanh hay chậm của vận tốc.

  Trong đó:

Δv: độ biến thiên vận tốc (m/s).

Δt: khoảng thời gian vận tốc biến thiên (s).

  Do đó, gia tốc a có đơn vị là m/s².

  Vậy, gia tốc là đại lượng đo bằng thương số giữa độ biến thiên Δv của vận tốc và khoảng thời gian Δt trong đó vận tốc biến thiên.

  * Chú ý :Vì chọn chiều + trục toạ độ cùng chiều chuyển động nên v₀ > 0, v > 0 và v > v₀ nên a > 0: gia tốc trong CĐTNDĐ luôn có giá trị dương và không đổi (a = hằng số).

  b) Vectơ gia tốc

 Vì vận tốc là đại lượng vectơ nên gia tốc cũng là đại lượng vectơ:

    (3.1b)

  Gia tốc là một đại lượng vectơ đặc trưng cho sự biến thiên nhanh hay chậm của vận tốc đo bằng tỷ số giữa độ biến thiên của vận tốc và khoảng thời gian xảy ra sự biến thiên đó.

  Vectơ gia tốc của chuyển động thẳng nhanh dần đều có:

- Gốc đặt tại vật chuyển động.

- Phương và chiều là phương và chiều của vectơ vận tốc.

- Độ dài biểu diễn độ lớn cả gia tốc theo một tỉ lệ xích nào đó.

Hình 3.4

 2. Vận tốc của chuyển động thẳng nhanh dần đều

  a) Công thức tính vận tốc

- Từ biểu thức gia tốc:

- Ta lấy gốc thời gian ở thời điểm t₀ (t₀ = 0) Þ Δt = t

Þ  

Û       (3.2)

Công thức (3.2) là công thức tính vận tốc của chuyển động thẳng nhanh dần đều. Nó cho ta biết vận tốc của vật ở những thời điểm khác nhau. Trong phương trình này v, v₀ và a luôn luôn cùng dấu.

Trong đó:

   v₀: vận tốc ban đầu của chất điểm tại thời điểm t₀.

   a: gia tốc của chất điểm.

   t: thời gian chất điểm thay đổi vận tốc từ v₀ đến v.

   v: vận tốc của chất điểm tại thời điểm t.

  b) Đồ thị vận tốc- thời gian

 Đồ thị biểu diễn sự phụ thuộc của vận tốc vào thời gian thể hiện trong phương trình (3. 4) gọi là đồ thị vận tốc. Đồ thị này có dạng một đoạn thẳng như hình vẽ, gia tốc a được biểu thị bằng hệ số góc của đường biểu diễn (Hình 3.5).

* Vận tốc trung bình

Hình 3.5

3. Công thức tính quãng đường đi được của CĐTNDĐ

 Gọi s là quãng đường vật chuyển động thẳng nhanh dần đều đi được trong thời gian t. Vận tốc trung bình của chuyển động là:

  Vì vận tốc tăng đều theo thời gian nên ta có thể chứng minh được công thức tính vận tốc trung bình sau đây:

Mặt khác: v = v_o + at

  Suy ra:

    (3.3)

Công thức (3.3) là công thức tính đường đi của chuyển động thẳng nhanh dần đều. Quãng đường đi trong chuyển động thẳng nhanh dần đều là một hàm số bậc hai của thời gian (Hình 3.6).

Hình 3.6. Đồ thị vận tốc - thời gian của một thang máy trong 4 giây đầu kể từ lúc chuyển động

 4. Công thức liên hệ giữa gia tốc, vận tốc, và quãng đường đi được của CĐTNDĐ

 Rút t từ các công thức (3.2) và (3.3) ta được:

    (3.4)

Bài tập ví dụ 1. Một người đi xe đạp bắt đầu khởi hành, sau 10 (s) đạt được tốc độ 2 (m/s). Hỏi gia tốc của người đó là bao nhiêu? Quãng đường đi được?

Tóm tắt:

- Cho biết:

t = 10 s

v = 2 m/s

- Tính: a = ? (m/s²), s = ? (m)

Giải:

 - Chọn hệ quy chiếu:

+ Hệ trục toạ độ:

Trục Ox trùng với quỹ đạo.

Gốc tọa độ O: tại vị trí vật bắt đầu chuyển động, có vận tốc v₀ = 0 (m/s).

Chiều dương (+) trục 0x: cùng chiều chuyển động.

+ Mốc thời gian(t₀ = 0): lúc vật ở 0.

Gia tốc của người đó là :

Quãng đường người đó đi được là:

Bài tập ví dụ 2. Một vật CĐTNDĐ với gia tốc a = 0,5 m/s², sau khi đi được quãng đường là 4 m kể từ lúc bắt đầu chuyển động thì vận tốc của vật sẽ bằng bao nhiêu? Sau khoảng thời gian bao nhiêu? Chọn chiều dương là chuyển động.

Tóm tắt:

a = 0,5 m/s²

v₀ = 0 m/s

s = 4 m.

- Tính:

v = ? t = ?

Giải:

v²- v₀² = 2as

Þ v =  = 2 (m/s)

v = v₀+ at

Bài tập ví dụ 3. Một vật CĐTNDĐ từ vận tốc 12m/s, sau đó khi đi được quãng đường 67,5m thì vận tốc bằng 15 m/s. Xác định gia tốc và thời gian của chuyển động.

Giải:

v- v₀² = 2as

= = 0,6 m/s²

v = v₀ + at

 5. Phương trình chuyển động của CĐTNDĐ

 Chất điểm M xuất phát từ một điểm A trên dường thẳng Ox, chuyển động nhanh dần đều theo chiều đương với vận tốc ban đầu v_o và với gia tốc a ( Hình 3.7) thì toạ độ của M tại thời điểm t là:

(3.5)

Phương trình (3.5) là phương trình toạ độ - thời gian (phương trình toạ độ) của chuyển động thẳng nhanh dần đều.

  Đồ thị toạ độ - thời gian ( Hình 3.8).

Hình 3.7

Hình 3.8. Đồ thị toạ độ - thời gian

Bài tập ví dụ 4. Hai ô tô chuyển động trên cùng một đường thẳng đi qua hai đia điểm A và B. Xe từ A chuyển động nhanh dần đều với gia tốc a₁ = 2 m/s² và vận tốc ban đầu v₀₁ = 5 m/s. Xe đi từ B chuyển động chậm dần đều với vận tốc ban đầu v₀₂ = 20 m/s và gia tốc a₂ = 2 m/s².

1. So sánh hướng gia tốc của 2 ô tô trong hai trường hợp: Hai xe chuyển động

+ cùng chiều

+  ngược chiều

2. Xác định vị trí và thời điểm hai xe gặp nhau trong hai trường hợp trên. Biết quảng đường AB dài  75 m.

Giải:

1. Xác định hướng gia tốc của 2 xe:

- Xe từ A chuyển động nhanh dần đều,  cùng chiều với , xe từ B chuyển động chậm dần đều,  ngược chiều với

+ Khi 2 xe chuyển động cùng chiều,  và  cùng chiều, nên  và  ngược chiều

+ Khi 2 xe chuyển động ngược chiều  và  ngược chiều , nên  và  cùng chiều

2. Chọn trục tọa độ Ox trùng với quỹ đạo AB, gốc tọa độ O tại A, chiều dương hướng từ A đến B, góc thời gian lúc hai xe qua A và B.

+ Phương trình chuyển động của xe 1: x₁ = 5t + t².

+ Phương trình chuyển động của xe 2:

- Khi chuyển động cùng chiều xe 1: x₂ = 75 + 20t – t².

                         Và khi chuyển động ngược chiều xe 1: x₂ = 75 - 20t + t².

- Khi 2 xe gặp nhau: x₁ = x₂.

+  Khi chuyển động cùng chiều : 5t + t²  = 75 + 20t – t².

Giải ra ta có: t = 10 s và t = - 2,5 s ( loại). Với t = 10 s thì x = 150 m.

Vậy sau 10 s thì xe 1 đuổi kịp xe 2 và ví trí gặp nhau cách A đoạn 150 m.

+ Khi chúng chuyển động ngược chiều : 5t + t² = 75 – 20t + t² => t = 3 s. Vậy khi chuyển động ngược chiều thì sau 3s chúng gặp nhau, vị trí gặp nhau, cách A đoạn x = 24 m.

III - CHUYỂN ĐỘNG THẲNG CHẬM DẦN ĐỀU

 1. Gia tốc của chuyển động thẳng chậm dần đều

  a) Công thức tính gia tốc

  Nếu chọn chiều của các vận tốc là chiều dương thì v < v₀. Gia tốc a có giá trị âm, nghĩa là ngược dấu với vận tốc.

  b) Véc tơ gia tốc

ngược hướng với  và .

  Vậy, trong chuyển động thẳng chậm dần đều, vectơ gia tốc luôn cùng phương, ngựoc chiều với vectơ vận tốc và có độ lớn không đổi.

Hình 3.9

 2. Vận tốc của chuyển động thẳng chậm dần đều

  a) Công thức tính vận tốc 

Chọn mốc thời gian là lúc vận tốc của vật bắt đầu giảm. Gọi v_olà vận tốc ban đầu, v là vận tốc tại thời điểm t, ta có:

v = v_o + at

    Trong đó, a ngược dấu với v và v₀

   (Nếu v₀ > v > 0, thì a < 0).

b) Đồ thị vận tốc – thời gian có dạng như ở Hình 3.10.

Hình 3.10

 3. Công thức tính quãng đường đi được và phương trình chuyển động của chuyển động thẳng chậm dần đều

  a) Công thức tính quãng đường đi được

    Trong đó, a ngược dấu với v₀ và s > 0.

  b) Phương trình chuyển động

  * Chú ý:

  - CĐTNDĐ: a cùng dấu v₀.

  - CĐTCDĐ: a ngược dấu v₀.