
Click để về mục lục
|
31 |
PHƯƠNG TRÌNH TRẠNG THÁI CỦA KHÍ LÝ TƯỞNG |
|
|
|
1. Kiến thức - Biết điều kiện áp dụng các định luật Bôi-lơ - Ma-ri-ốt và định luật Sác-lơ. - Nêu được định nghĩa quá trình đẳng áp, viết được biểu thức liên hệ giữa thể tích và nhiệt độ tuyệt đối trong quá trình đẳng áp và nhận được dạng đường đẳng áp trong hệ tọa độ (p, T) và (p, t). 2. Kỹ năng - Hiểu ý nghĩa vật lí của “độ không tuyệt đối”. - Từ các phương trình của định luật Bôi-lơ - Ma-ri-ốt và định luật Sác - lơ xây dựng được phương trình Cla-pê-rôn và từ biểu thức của phương trình này viết được biểu thức đặc trưng cho các đẳng quá trình. - Vận dụng được phương trình Cla-pê-rông để giải được các bài tập ra trong bài và bài tập tương tự. |
|
|
|
I - KHÍ THỰC VÀ KHÍ LÍ TƯỞNG
Các thí nghiệm chính xác cho thấy, các chất khí thực chỉ tuân theo gần
đúng các định luật
Bôi-lơ – Ma-ri-ốt và định luật
Sác-lơ. Giá trị của tích pV và thương
Sự khác biệt giữa khí thực và khí lí tưởng không lớn ở nhiệt độ và áp suất thông thường. |
* Ta nói một chất khí ở trạng thái khí lý tưởng khi các lực tương tác, lực liên kết giữa các phân tử (lực Van der Waals) hoàn toàn bằng không. Chất khí càng gần trạng thái lý tưởng khi mật độ của nó càng thấp, nghĩa là khi áp suất càng thấp hay nhiệt độ càng cao.
|
|
|
II - PHƯƠNG TRÌNH TRẠNG THÁI (PTTT) CỦA KHÍ LÝ TƯỞNG Phương trình xác định mối liên hệ giữa ba thông số trạng thái của chất khí gọi là phương trình trạng thái của khí lí tưởng. Để lập phương trình này, ta xét một lượng khí từ trạng thái 1 (p1, V1, T1) sang trạng thái 2 (p2, V2, T2) qua trạng thái trung gian 1' (p', V2, T1) bằng các đẳng quá trình đã học trong các bài trước (Hình 31.1). Ta dễ dàng chứng minh được:
Phương trình (31.1) trên được nhà vật lí người Pháp Cla-pê-rôn (Clapeyron, 1799 - 1864) đưa ra năm 834 và được gọi là phương trình trạng thái của khí lí tưởng hay phương trình Cla-pê-rôn. Đối với một khối lượng khí đã cho, tích áp suất và thể tích chia cho nhiệt độ tuyệt đối là một đại lượng không đổi. |
Hình 31.1
|
|
|
III - QUÁ TRÌNH ĐẲNG ÁP 1. Quá trình đẳng áp Quá trình biến đổi trạng thái khi áp suất không đổi gọi là quá trình đẳng áp. 2. Liên hệ giữa thể tích và nhiệt độ tuyệt đối trong quá trình đẳng áp Từ công thức (29.2):
Khi p1 = p1 thì: (31.2)
Trong quá trình đẳng áp của một lượng khí nhất định, thể tích tỉ lệ thuận với nhiệt độ tuyệt đối. |
|
|
|
3. Đường đẳng áp a) Định nghĩa Đường biểu diễn sự biến thiên của thể tích theo nhiệt độ khi áp suất không đổi gọi là đường đẳng áp. b) Đặc điểm Trong hệ toạ độ (V,T) đường đẳng áp là đường thẳng kéo dài đi qua góc toạ độ. (Hình 31.2) Ứng với các thể tích khác nhau của cùng một lượng khí ta có những đường đẳng áp khác nhau. Đường ở trên có áp suất nhỏ hơn. |
Hình 31.2
|
|
|
IV - "ĐỘ KHÔNG TUYỆT ĐỐI" Độ không tuyệt đối: T = 0K tương ứng với t = -2730C (chính xác hơn là khoảng -273,150C) (Hình 31.3). Nhiệt độ thấp nhất mà con người thực hiện được trong phòng thí nghiệm hiện nay là 10-9 K. |
Nếu sử dụng nhiệt độ
xensius, ta có:
Hình 31.3. loại nhiệt giai |
|
|
|
Bài tập ví dụ. Một quả bóng thám không có thể tích V1 = 200 l ở nhiệt độ t1 = 270 C trên mặt đất. Bóng được thả ra và bay lên đến độ cao mà ở đó áp suất khí quyển chỉ còn bằng 0,6 áp suất khí quyển ở mặt đất và nhiệt độ t2 = 50C. Tính thể tích của quả bóng ở độ cao đó (Bỏ qua áp suất phụ gây ra bởi vỏ bóng). Giải: Áp dụng
phương trình trạng thái:
Þ
V2 = V1 Ở nhiệt độ 273oC thể tích của một lượng khí là 10 lít. Tính thể tích lượng khí đó ở 5460C khi áp suất không đổi. Vì p =
const nên Suy ra V2 = 15lít
Đồ thị bên cho biết chu trình biến đổi trạng thái của một lượng khí lý tưởng được biểu diễn trong hệ toạ độ(p,T): a, Nêu tên gọi của các quá trình:1-2,2-3 và 3-1. b, Hãy biểu diễn chu trình trên trong hệ toạ độ(V,T). Giải: a. Các quá trình : + 1-2 : đẳng áp + 2-3 : đẳng nhiệt + 3-1 : đẳng tích b. Đồ thị :
|
|
Phương trình trạng thái cúa khí lý tưởng:
T1 = T2
Vl = V2
p1 = p1
|

Câu 1. Khí lí tưởng là gì?
Câu 2. Lập phương trình trạng thái của khí lí tưởng.
Câu 3. Viết biểu thức của sự nở đẳng áp của chất khí. Hệ số nở đẳng áp của các chất khí có đặc điểm gì?
![]()
31.1. Ghép nội dung ở cột bên trái với nội dung tương ứng ở cột bên phải dể thành một câu có nội dung đúng.
|
1. Phương trình trạnh thái của khí lí tưởng |
a) định luật gần đúng. |
|
2. Định luật Bôi-lơ – Ma-ri-ốt là |
b) đường thẳng kéo dài đi qua gốc tọa độ cũa hệ tọa độ(V,T). |
|
3. Quá trình đẳng áp là |
c) – 2730C. |
|
4. Đường đẳng áp là |
d) sự chuyển trạng thái của chất khí khi áp suất không đổi. |
|
5. Độ không tuyệt đối là |
đ) thiết lập mối liên hệ giữa cả ba thông số trạng thái của một lượng khí. |
31.2. Hệ thức nào sau đây KHÔNG PHÙ HỢP với phương trình trạng thái của khí lí tưởng?
A.
![]() =
hằng số. B.
=
hằng số. B.
![]() .
.
31.3. Hệ thức nào sau đây KHÔNG PHÙ HỢP với quá trình đẳng áp?
A.
![]() =
hằng số B.
=
hằng số B.
![]()
31.4. Đồ thị nào sau đây phù hợp với quá trình đẳng áp?
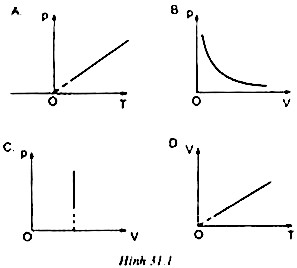
31.5. Trong quá trình nào sau đây, cả ba thông số trạng thái của một lượng khí xác định đều thay đổi?
A. Không khí bị đun nóng trong một bình đậy kín.
B. Không khí trong một quả bóng bàn bị một học sinh dùng tay bóp dẹp.
C. Không khí trong một xilanh được đun nóng, dãn nở và đầy pit – tông dịch chuyển.
D. Trong ba hiện tượng trên.
31.6. Một lượng khí đựng trong một xilanh có pit – tông chuyển động được. Các thông số trạng thái của lượng khí này là : 2 atm , 15 lít , 300 K. Khi pit – tông nén khí, áp suất của khí tăng lên tới 3,5 atm, thể tích giảm còn 12 lít. Xác định nhiệt độ của khí nén.
31.7*. Tính khối lượng riêng của không khí ở 1000C và áp suất 2.105 Pa. Biết khối lượng riêng của không khí ở 00C và 1,01.105 Pa là 1,29.kg/m3.

HẰNG SỐ CỦA KHÍ LÍ TƯỞNG
1. Điều kiện chuẩn
Người ta quy ước điều kiện chuẩn về nhiệt độ và áp suất như sau :
to = 0o C ![]() To = 273K
To = 273K
po = 760 mmHg ![]() po = l,013.l05
Pa
po = l,013.l05
Pa
2. Hằng số của khí lí tưởng
Ta có thể xác định được giá trị
của hằng số trong phương trình ![]() = const đối với 1 mol khí ở điều kiện
chuẩn. Khi đó:
= const đối với 1 mol khí ở điều kiện
chuẩn. Khi đó:
![]()
R có giá trị chung cho mọi khí lí tưởng và được gọi là hằng số của khí lí tưởng. Đơn vị của R là J/mol.K.
PHƯƠNG TRÌNH CLA-PÊ-RÔN - MEN-ĐÊ-LÊ-ÉP
Phương trình Cla-pê-rôn dùng để giải các bài toán về trạng thái của một lượng khí không đổi. Nhà bác học người Nga Mendeleev (1834 ~ 1907) đã dựa vào phương trình này để xây dựng phương trình cho phép giải được những bài toán trong đó lượng khí thay đổi. Đó là phương trình Cla-pê-rôn - Men-đê-lê-ép.
Phương trình Cla-pê-rôn viết cho một mol khí:
![]()
Với
m: Khối lượng của khí (kg);
![]() : Khối lượng của một mol khí , gọi là
khối lượng mol (kg/mol);
: Khối lượng của một mol khí , gọi là
khối lượng mol (kg/mol);
![]() : số mol khí;
: số mol khí;
v: thể tích của một mol khí, gọi là thể tích mol (m3/mol).
Thể tích của lượng khí có khối
lượng m là: V = ![]() v
v
Từ phương trìmh Cla-pê-rôn và những đại lượng nêu trên ta chứng minh được phương trình:
![]()